题目内容
20.某女士为将体重维持在正常水平,每天坚持体育锻炼.已知该女士某星期一测得其体重是50kg,而后每天测得的体重与前一天相比,或减少0.5kg或维持不变或增加0.5kg,若该星期天该女士测得其体重仍然是50kg,则该女士在这个星期内每天测得的体重的所有可能结果有( )| A. | 121种 | B. | 141种 | C. | 231种 | D. | 282种 |
分析 星期一和星期天的体重相同,所以从这周的第二天开始的中间“减少0.5kg”或“增加0.5kg”的天数必须相同,都是0、1、2、3天,共四种情况,利用组合知识可得结论
解答 解:星期一和星期天的体重相同,所以从这周的第二天开始的中间“减少0.5kg”或“增加0.5kg”的天数必须相同,都是0、1、2、3天,共四种情况
当为0天时,故有${C}_{6}^{0}$=1种,
当有1天时,故有${C}_{6}^{1}•{C}_{5}^{1}$=30种,
当有2天时,故有${C}_{6}^{2}•{C}_{4}^{2}$=90种,
当有3天时,故有${C}_{6}^{3}•{C}_{3}^{3}$=20,
根据分类计数原理可得,1+30+09+20=141种,
故选:B.
点评 本题考查组合知识的运用,考查学生分析解决问题的能力,确定中间“减少0.5kg”或“增加0.5kg”的天数必须相同是关键

练习册系列答案
相关题目
11.已知函数f(x)=2sin(2x+φ)(|φ|<$\frac{π}{2})$的图象过点$(0,\sqrt{3})$,则f(x)的图象的一个对称中心是( )
| A. | $(-\frac{π}{3},0)$ | B. | $(-\frac{π}{6},0)$ | C. | $(\frac{π}{6},0)$ | D. | $(\frac{π}{4},0)$ |
12.设a,b为两条不同的直线,α,β为两个不重合的平面.下列命题中正确的是( )
| A. | 若α⊥β,a⊥α,则a∥β | |
| B. | 若a,b与α所成的角相等,则a与b平行或相交 | |
| C. | 若α内有三个不共线的点到β的距离相等,则α∥β | |
| D. | 若α∩β=b,a?α且a∥β,则a∥b |
10.将函数f(x)=sinxcosx的图象向左平移$\frac{π}{4}$个长度单位,得到函数g(x)的图象,则g(x)的单调递增区间是( )
| A. | $({kπ-\frac{π}{2},kπ})({k∈Z})$ | B. | $({kπ,kπ+\frac{π}{2}})({k∈Z})$ | C. | $({kπ-\frac{π}{4},kπ+\frac{π}{4}})({k∈Z})$ | D. | $({kπ+\frac{π}{4},kπ+\frac{3}{4}π})({k∈Z})$ |
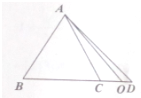 如图,在△ABC中,点D是BC延长线上的点,$\overline{BC}$=3$\overline{CD}$,O在线段CD上且不与端点重合,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+(1-x)$\overrightarrow{AC}$,则x的取值范围是($-\frac{1}{3}$,0).
如图,在△ABC中,点D是BC延长线上的点,$\overline{BC}$=3$\overline{CD}$,O在线段CD上且不与端点重合,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+(1-x)$\overrightarrow{AC}$,则x的取值范围是($-\frac{1}{3}$,0).


