题目内容

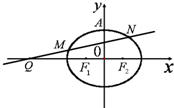如图，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点为F1，F2，其上顶点为A．已知△F1AF2是边长为2的正三角形．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点Q（-4，0）任作一动直线l交椭圆C于M，N两点，记
MQ
=-λ•
QN
若在线段MN上取一点R，使得
MR
=λ•
RN
，试判断当直线l运动时，点R是否在某一定直线上运动？若在，请求出该定直线的方程；若不在，请说明理由．
分析：（Ⅰ）由△F1AF2是边长为2的正三角形，可得c=1，a=2，从而可求b，即可得到椭圆C的方程；
（Ⅱ）设直线方程与椭圆方程联立，利用韦达定理，由
MQ
=-λ•
QN
，确定λ的值，由
MR
=λ•
RN
，可得R的横坐标为定值，即可得到结论．
解答：解：（Ⅰ）∵已知△F1AF2是边长为2的正三角形，∴c=1，a=2，…（2分）
∴b=
a2-c2
=
3

∴椭圆C的方程为
x2
4
+
y2
3
=1．…（4分）
（Ⅱ）直线MN的斜率必存在，设其直线方程为y=k（x+4），并设M（x1，y1），N（x2，y2）．
直线方程与椭圆方程联立，消去y得（3+4k2）x2+32k2x+64k2-12=0，则
△=144（1-4k2）＞0，x1+x2=
-32k2
3+4k2
，x1x2=
64k2-12
3+4k2
  …（7分）
由
MR
=λ•
RN
，得-4-x1=λ（x2+4），故λ=-
x1+4
x2+4
．…（9分）
设点R的坐标为（x0，y0），则由
MQ
=-λ•
QN
得x0-x1=-λ（x2-x0），解得
x0=
x1-λx2
1-λ
=
x1+
x1+4
x2+4
×x2
1+
x1+4
x2+4
=
2x1x2+4(x1+x2)
(x1+x2)+8

=
2×
64k2-12
3+4k2
+4×
-32k2
3+4k2
-32k2
3+4k2
+8
=-1．…（13分）
故点R在定直线x=-1上．…（14分）
点评：本题考查椭圆方程，考查直线与椭圆的位置关系，考查向量知识的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
精英家教网如图，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．
（1）已知椭圆C1：
x2
4
+y2=1和C2：
x2
16
+
y2
4
=1，判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；
（2）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．
如图，已知椭圆C：
x2
a2
+
y2
b2
=1的离心率为
3
2
，过椭圆C上一点P（2，1）作倾斜角互补的两条直线，分别与椭圆交于点A、B，直线AB与x轴交于点M，与y轴负半轴交于点N．
（Ⅰ）求椭圆C的方程：
（Ⅱ）若S△PMN=
3
2
，求直线AB的方程．
如图，已知椭圆C：
x2
36
+
y2
20
=1的左顶点，右焦点分别为A，F，右准线为l，N为l上一点，且在x轴上方，AN与椭圆交于点M．
（1）若AM=MN，求证：AM⊥MF；
（2）过A，F，N三点的圆与y轴交于P，Q两点，求PQ的最小值．
（2012•深圳一模）如图，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
3
2
，以椭圆C的左顶点T为圆心作圆T：（x+2）2+y2=r2（r＞0），设圆T与椭圆C交于点M与点N．
（1）求椭圆C的方程；
（2）求
TM
•
TN
的最小值，并求此时圆T的方程；
（3）设点P是椭圆C上异于M，N的任意一点，且直线MP，NP分别与x轴交于点R，S，O为坐标原点，求证：|OR|•|OS|为定值．
精英家教网如图，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左顶点，右焦点分别为A、F，右准线为m．圆D：x2+y2+x-3y-2=0．
（1）若圆D过A、F两点，求椭圆C的方程；
（2）若直线m上不存在点Q，使△AFQ为等腰三角形，求椭圆离心率的取值范围．
（3）在（1）的条件下，若直线m与x轴的交点为K，将直线l绕K顺时针旋转
π
4
得直线l，动点P在直线l上，过P作圆D的两条切线，切点分别为M、N，求弦长MN的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网