题目内容
已知双曲线 =1(m>0,n>0)的顶点为A1、A2,与y轴平行的直线l交双曲线于点P、Q.
=1(m>0,n>0)的顶点为A1、A2,与y轴平行的直线l交双曲线于点P、Q.
(1)求直线A1P与A2Q交点M的轨迹方程;
(2)当m≠n时,求所得圆锥曲线的焦点坐标、准线方程和离心率.
 =1(m>0,n>0)的顶点为A1、A2,与y轴平行的直线l交双曲线于点P、Q.
=1(m>0,n>0)的顶点为A1、A2,与y轴平行的直线l交双曲线于点P、Q. (1)求直线A1P与A2Q交点M的轨迹方程;
(2)当m≠n时,求所得圆锥曲线的焦点坐标、准线方程和离心率.

(1)=1, M的轨迹方程是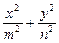 (2)(ⅰ)当m>n时,焦点坐标为(±
(2)(ⅰ)当m>n时,焦点坐标为(±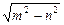 ,0),准线方程为x=±
,0),准线方程为x=±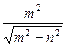 ,离心率e=
,离心率e=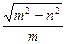 ;
;
(ⅱ)当m<n时,焦点坐标为(0,±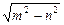 ),准线方程为y=±
),准线方程为y=±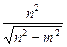 ,离心率e=
,离心率e= .
.
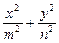 (2)(ⅰ)当m>n时,焦点坐标为(±
(2)(ⅰ)当m>n时,焦点坐标为(±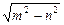 ,0),准线方程为x=±
,0),准线方程为x=±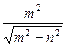 ,离心率e=
,离心率e=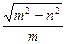 ;
;(ⅱ)当m<n时,焦点坐标为(0,±
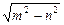 ),准线方程为y=±
),准线方程为y=±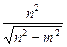 ,离心率e=
,离心率e= .
.(1)设P点的坐标为(x1,y1),则Q点坐标为(x1,-y1),又有A1(-m,0),A2(m,0),则A1P的方程为: y=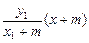 ①
①
A2Q的方程为: y=-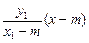 ②
②
①×②得: y2=-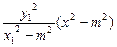 ③
③
又因点P在双曲线上,故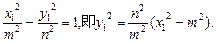
代入③并整理得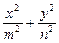 =1, 此即为M的轨迹方程.
=1, 此即为M的轨迹方程.
(2)当m≠n时,M的轨迹方程是椭圆.
(ⅰ)当m>n时,焦点坐标为(±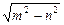 ,0),准线方程为x=±
,0),准线方程为x=±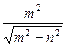 ,离心率e=
,离心率e=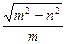 ;
;
(ⅱ)当m<n时,焦点坐标为(0,±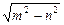 ),准线方程为y=±
),准线方程为y=±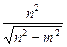 ,离心率e=
,离心率e= .
.
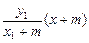 ①
①A2Q的方程为: y=-
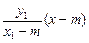 ②
②①×②得: y2=-
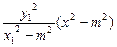 ③
③又因点P在双曲线上,故
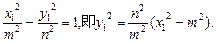
代入③并整理得
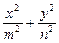 =1, 此即为M的轨迹方程.
=1, 此即为M的轨迹方程. (2)当m≠n时,M的轨迹方程是椭圆.
(ⅰ)当m>n时,焦点坐标为(±
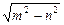 ,0),准线方程为x=±
,0),准线方程为x=±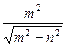 ,离心率e=
,离心率e=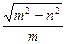 ;
;(ⅱ)当m<n时,焦点坐标为(0,±
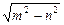 ),准线方程为y=±
),准线方程为y=±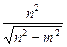 ,离心率e=
,离心率e= .
.
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
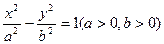 的右顶点为E,双曲线的左准线与该双曲线的两渐近线的交点分别为A、B两点,若∠AEB=60°,则该双曲线的离心率e是()
的右顶点为E,双曲线的左准线与该双曲线的两渐近线的交点分别为A、B两点,若∠AEB=60°,则该双曲线的离心率e是()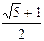
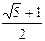 或2
或2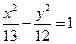 上一点
上一点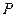 到右焦点的距离等于
到右焦点的距离等于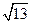 ,那么点
,那么点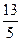
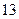
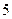
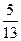
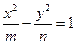 的一条渐近线方程为
的一条渐近线方程为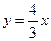 ,则该双曲线的离心率
,则该双曲线的离心率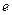 为 .
为 .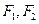 是双曲线
是双曲线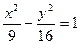 的两个焦点,点
的两个焦点,点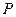 在双曲线上,且
在双曲线上,且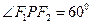 ,
,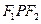 的面积。
的面积。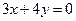 ,一焦点为(4,0)的双曲线标准方程是
,一焦点为(4,0)的双曲线标准方程是 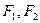 是双曲线
是双曲线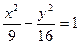 的两个焦点,点P在双曲线上且满足
的两个焦点,点P在双曲线上且满足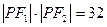 ,
,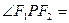 ————
————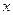 、
、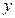 满足条件
满足条件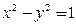 ,则
,则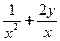 的取值范围是___________________.
的取值范围是___________________.