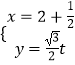题目内容
【题目】
已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() 存在极小值
存在极小值![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,如果存在两个不相等的正数
时,如果存在两个不相等的正数![]() ,使得
,使得![]() ,求证:
,求证:![]() .
.
请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
【答案】见解析
【解析】(1)由题可得![]() ,
,
依题意![]() ,即
,即![]() ,解得
,解得![]() .(2分)
.(2分)
(2)由(1)知![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,无极值;
上单调递增,无极值;
当![]() 时,
时,![]() 时
时![]() ,
,![]() 时
时![]() ,
,
故![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,
,
所以函数![]() 的极小值为
的极小值为![]() .(4分)
.(4分)
当![]() 时,
时,![]() ,即
,即![]() ,即
,即![]() 恒成立.(5分)
恒成立.(5分)
令![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() ,且当
,且当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
故![]() 为
为![]() 在
在![]() 上唯一的极大值点,也是最大值点,
上唯一的极大值点,也是最大值点,
所以![]() ,所以
,所以![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .(7分)
.(7分)
(3)由(2)知,当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
设![]() ,则一定有
,则一定有![]() .(8分)
.(8分)
构造函数![]() ,
,![]() .(9分)
.(9分)
则![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,所以
,所以![]() .(10分)
.(10分)
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为函数![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以![]() .(12分)
.(12分)

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
【题目】“累计净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为![]() 时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
累计净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
已知某批空气净化器共![]() 台,其累计净化量都分布在区间
台,其累计净化量都分布在区间![]() 内,为了解其质量,随机抽取了
内,为了解其质量,随机抽取了![]() 台净化器作为样本进行估计,按照
台净化器作为样本进行估计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均匀分组,其中累计净化量在
均匀分组,其中累计净化量在![]() 的所有数据有:
的所有数据有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,并绘制了如下频率分布直方图.
,并绘制了如下频率分布直方图.
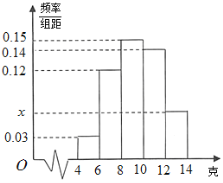
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共2000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累计净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.