Question

15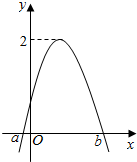．如图是函数f（x）=Asin（2x+φ）（A＞0，|φ|≤$\frac{π}{2}$）图象的一部分，对不同的x₁，x₂∈[a，b]，若f（x₁）=f（x₂），有f（x₁+x₂）=$\sqrt{3}$，则φ的值为$\frac{π}{3}$．

Answer 1

分析 由最大值求出A，结合图象可得a+b=x₁ +x₂ ．由五点法作图求得a+b=$\frac{π}{2}$-φ，由f（a+b）=2sinφ=f（x₁ +x₂ ）=$\sqrt{3}$，可得sinφ的值，从而求得φ的值．

解答 解：根据函数f（x）=Asin（2x+φ）（A＞0，|φ|≤$\frac{π}{2}$）图象的一部分，
可得A=2，周期为$\frac{2π}{2}$=π，∴b-a=$\frac{π}{2}$．
由f（x₁）=f（x₂），可得函数的图象关于直线x=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{a+b}{2}$对称，故a+b=x₁ +x₂ ．
由五点法作图可得2a+φ=0，2b+φ=π，∴a+b=$\frac{π}{2}$-φ．
结合f（a+b）=f（$\frac{π}{2}$-φ）=2sin（π-2φ+φ）=2sinφ=f（x₁ +x₂ ）=$\sqrt{3}$，可得sinφ=$\frac{\sqrt{3}}{2}$，
∴φ=$\frac{π}{3}$，
故答案为：$\frac{π}{3}$．

点评 本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，函数y=Asin（ωx+φ）的图象特征，属于中档题．