题目内容
10.已知数列{an}中,a1=$\frac{4}{3}$,且有an+1=an2-an+1,n∈N*(I)求证:数列{an}是递增数列;
(Ⅱ)记Sn=$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+…+\frac{1}{{a}_{n}}$,Tn=$\frac{1}{{a}_{1}}•\frac{1}{{a}_{2}}•…•\frac{1}{{a}_{n}}$求证:Sn+3Tn=3.
分析 (I)由an+1=an2-an+1,n∈N*,an≠1,可得an+1-an=$({a}_{n}-1)^{2}$>0,即可证明.
(II)由an+1=an2-an+1,n∈N*,可得an+1-1=an(an-1),取倒数可得:$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n}-1}$-$\frac{1}{{a}_{n+1}-1}$.利用“裂项求和”可得Sn=$\frac{1}{{a}_{1}-1}$-$\frac{1}{{a}_{n+1}-1}$.另一方面:由an+1-1=an(an-1),可得$\frac{1}{{a}_{n}}$=$\frac{{a}_{n}-1}{{a}_{n+1}-1}$,因此Tn=$\frac{{a}_{1}-1}{{a}_{n+1}-1}$,即可证明.
解答 证明:(I)∵an+1=an2-an+1,n∈N*,an≠1,
∴an+1-an=$({a}_{n}-1)^{2}$>0,
∴an+1>an.
∴数列{an}是递增数列.
(II)∵an+1=an2-an+1,n∈N*,
∴an+1-1=an(an-1),
∴$\frac{1}{{a}_{n+1}-1}=\frac{1}{{a}_{n}-1}-\frac{1}{{a}_{n}}$,
∴$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n}-1}$-$\frac{1}{{a}_{n+1}-1}$.
∴Sn=$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+…+\frac{1}{{a}_{n}}$=$(\frac{1}{{a}_{1}-1}-\frac{1}{{a}_{2}-1})$+$(\frac{1}{{a}_{2}-1}-\frac{1}{{a}_{3}-1})$+…+$(\frac{1}{{a}_{n}-1}-\frac{1}{{a}_{n+1}-1})$
=$\frac{1}{{a}_{1}-1}$-$\frac{1}{{a}_{n+1}-1}$
=3-$\frac{1}{{a}_{n+1}-1}$.
由an+1-1=an(an-1),
可得$\frac{1}{{a}_{n}}$=$\frac{{a}_{n}-1}{{a}_{n+1}-1}$,
∴Tn=$\frac{1}{{a}_{1}}•\frac{1}{{a}_{2}}•…•\frac{1}{{a}_{n}}$=$\frac{{a}_{1}-1}{{a}_{2}-1}$•$\frac{{a}_{2}-1}{{a}_{3}-1}$•…•$\frac{{a}_{n}-1}{{a}_{n+1}-1}$=$\frac{{a}_{1}-1}{{a}_{n+1}-1}$=$\frac{1}{3({a}_{n+1}-1)}$,
∴Sn+3Tn=3-$\frac{1}{{a}_{n+1}-1}$+$\frac{3}{3({a}_{n+1}-1)}$=3.
∴Sn+3Tn=3.
点评 本题考查了递推关系的应用、“裂项求和”、“累乘求积”,考查了变形能力、推理能力与计算能力,属于难题.

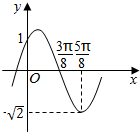 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ≤$\frac{π}{2}$)的图象如图所示,将f(x)的图象向左平移$\frac{π}{8}$个单位后得到函数g(x)的图象,则( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ≤$\frac{π}{2}$)的图象如图所示,将f(x)的图象向左平移$\frac{π}{8}$个单位后得到函数g(x)的图象,则( )| A. | g(x)=$\sqrt{2}$sin(2x+$\frac{3π}{8}$) | B. | g(x)=$\sqrt{2}$cos2x | C. | g(x)=$\sqrt{2}$cos(2x+$\frac{3π}{8}$) | D. | g(x)=$\sqrt{2}$sin2x |
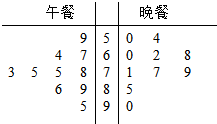
(1)根据茎叶图计算学生对食堂午餐评分的平均值;
(2)根据学生的评分,将学生对食堂的评分分为三个等级:
| 评分 | 低于65分 | 65分到85分 | 高于85分 |
| 评价等级 | 差 | 正常 | 优 |
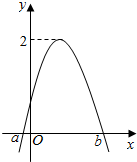 如图是函数f(x)=Asin(2x+φ)(A>0,|φ|≤$\frac{π}{2}$)图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则φ的值为$\frac{π}{3}$.
如图是函数f(x)=Asin(2x+φ)(A>0,|φ|≤$\frac{π}{2}$)图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则φ的值为$\frac{π}{3}$.