题目内容
4.若$\frac{2sinα+cosα}{2cosα-sinα}$=2,求sinα+cosα的值及2sinαcosα+cos2α-2的值.分析 由$\frac{2sinα+cosα}{2cosα-sinα}$=2,化弦为切求得tanα的值,然后分α的象限求得sinα+cosα的值;再把2sinαcosα+cos2α-2化切后得答案.
解答 解:由$\frac{2sinα+cosα}{2cosα-sinα}$=2,得$\frac{2tanα+1}{2-tanα}=2$,解得:tan$α=\frac{3}{4}$.
若α是第一象限角,则cosα=$\frac{1}{secα}=\frac{1}{\sqrt{1+ta{n}^{2}α}}$=$\frac{1}{\sqrt{1+(\frac{3}{4})^{2}}}=\frac{4}{5}$,
sin$α=\sqrt{1-co{s}^{2}α}=\sqrt{1-(\frac{4}{5})^{2}}=\frac{3}{5}$.
∴sinα+cosα=$\frac{3}{5}+\frac{4}{5}=\frac{7}{5}$;
若α是第三象限角,则cosα=$-\frac{4}{5}$,sin$α=-\frac{3}{5}$,sinα+cosα=-$\frac{7}{5}$;
2sinαcosα+cos2α-2=2sinαcosα+cos2α-2sin2α-2cos2α
=2sinαcosα-2sin2α-cos2α=$\frac{2sinαcosα-2si{n}^{2}α-co{s}^{2}α}{si{n}^{2}α+co{s}^{2}α}$
=$\frac{2tanα-2ta{n}^{2}α-1}{ta{n}^{2}α+1}$=$\frac{2×\frac{3}{4}-2×(\frac{3}{4})^{2}-1}{(\frac{3}{4})^{2}+1}$=$-\frac{2}{5}$.
点评 本题考查三角函数的化简与求值,考查了同角三角函数基本关系式的应用,是基础的计算题.

 阅读快车系列答案
阅读快车系列答案| A. | 4 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$或2 | D. | 2$\sqrt{2}$或4 |
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 1 | D. | -1 |
| A. | -3 | B. | $\frac{1}{3}$ | C. | -2 | D. | 0 |
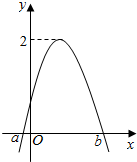 如图是函数f(x)=Asin(2x+φ)(A>0,|φ|≤$\frac{π}{2}$)图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则φ的值为$\frac{π}{3}$.
如图是函数f(x)=Asin(2x+φ)(A>0,|φ|≤$\frac{π}{2}$)图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则φ的值为$\frac{π}{3}$.