题目内容
9.方程(lga+lgx)•(lga+2lgx)=4有两个小于1的正根α,β.(1)若lgα+lgβ=-$\frac{9}{2}$,求a的值;
(2)若|lgα-lgβ|≤2$\sqrt{3}$,求实数a的取值范围.
分析 (1)将已知方程转化为一般式方程,然后由根与系数的关系来求a的值;
(2)利用根与系数的关系和对数的运算性质将|lgα-lgβ|≤2$\sqrt{3}$转化为关于a的不等式,通过解不等式求得a的取值范围.
解答 解:由方程(lga+lgx)•(lga+2lgx)=4有两个小于1的正根α,β,得
2lg2x+3lgalgx+lg2a-4=0.
(1)∵α,β是方程(lga+lgx)•(lga+2lgx)=4,即2lg2x+3lgalgx+lg2a-4=0的两个正根,
∴lgα+lgβ=-$\frac{3}{2}$lga=-$\frac{9}{2}$,
∴lga=3,
则a=1000;
(2)∵lgα+lgβ=-$\frac{3}{2}$lga,lgα•lgβ=$\frac{l{g}^{2}a-4}{2}$,
∴|lgα-lgβ|2=(lgα+lgβ)2-4lgα•lgβ≤12,
∴$\frac{9}{4}$lg2a-2lg2a+8≤12,
解得-4≤lga≤4,
又∵方程(lga+lgx)•(lga+2lgx)=4有两个小于1的正根α,β,
∴lga>0且lgα•lgβ=$\frac{l{g}^{2}a-4}{2}$>0,
解得lga>2,
∴2<lga≤4
∴实数a的取值范围是(100,10000].
点评 本题考查了对数的运算性质和根的存在性及根的个数判断.还考查运算能力,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
16.化简(cos47°30′-sin47°30′)(sin23°cos8°-sin67°sin8°)=( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 1 | D. | -1 |
13.已知变量x、y满足约束条件$\left\{\begin{array}{l}{|x|≤y}\\{x+2y-1≤0}\end{array}\right.$,则目标函数z=2x-y的最小值为( )
| A. | -3 | B. | $\frac{1}{3}$ | C. | -2 | D. | 0 |
14.设函数y=sinx在区间$[t,t+\frac{π}{2}]$上的最大值为M(t),最小值为m(t),则M(t)-m(t)的最小值和最大值分别为( )
| A. | 1,2 | B. | $1,\sqrt{2}$ | C. | $1-\frac{{\sqrt{2}}}{2},1$ | D. | $1-\frac{{\sqrt{2}}}{2},\sqrt{2}$ |
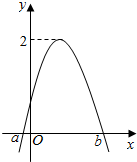 如图是函数f(x)=Asin(2x+φ)(A>0,|φ|≤$\frac{π}{2}$)图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则φ的值为$\frac{π}{3}$.
如图是函数f(x)=Asin(2x+φ)(A>0,|φ|≤$\frac{π}{2}$)图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有f(x1+x2)=$\sqrt{3}$,则φ的值为$\frac{π}{3}$.