Question

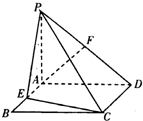如图，PA⊥平面ABCD，四边形ABCD是矩形，E、F分别是AB，PD的中点．
（Ⅰ）求证：AF∥平面PCE；
（Ⅱ）若PA=AD且AD=2，CD=3，求P-CE-A的正切值．

Answer 1

分析：（Ⅰ）取PC中点M，连ME，MF，利用三角形的中位线证明四边形AFME为平行四边形，从而证明AF∥平面PCE．
（Ⅱ）延长DA，CE交于N，连接PN，过A作AH⊥CN于H连PH．利用PA⊥平面ABCD，根据三垂线定理可得PH⊥CN，从而可知∠PHA为二面角P-EC-A的平面角，进而可求其正切值．

解答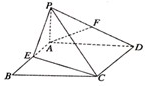：证明：（Ⅰ）取PC中点M，连ME，MF
∵FM∥CD，FM=

1

2

CD，AE∥CD，AE=

1

2

CD
∴AE∥FM，且AE=FM，即四边形AFME是平行四边形
∴AF∥EM，
∵AF?平面PCE
∴AF∥平面PCE…（6分）
（Ⅱ）延长DA，CE交于N，连接PN，过A作AH⊥CN于H连PH．
∵PA⊥平面ABCD，∴PH⊥CN（三垂线定理）
∴∠PHA为二面角P-EC-A的平面角…（8分）
∵AD=2，CD=3
∴CN=5，即EN=

5

2

，PA=AD
∴PA=2，∴AH=

AN•AE

EN

=

2• 3 2

5 2

=

6

5

∴tan∠PHA=

PH

AH

=

2

6 5

=

5

3

∴二面角P-EC-A的正切值为

5

3

．…（12分）

点评：本题以线面垂直为载体，考查直线和平面平行的判定，考查面面角，解题的关键是正确运用线面平行的判定定理，正确作出面面角．