题目内容
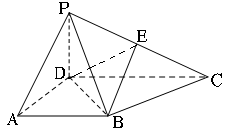
正方体ABCD-A1B1C1D1中,二面角C1-AB-C的平面角等于________.
解析试题分析: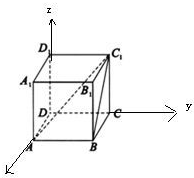
解:如图,设正方体ABCD-A1B1C1D1的棱长为1,以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,则A(1,0,0),B(1,1,0),C1(0,1,1),∴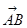 =(0,1,0),
=(0,1,0),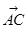 =(-1,1,1),设面ABC1的法向量为
=(-1,1,1),设面ABC1的法向量为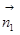 =(x,y,z),∵
=(x,y,z),∵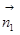 •
•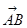 =0,
=0,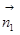 •
•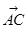 =0,∴y=0,-x+y+z=0,∴
=0,∴y=0,-x+y+z=0,∴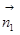 =(1,0,1),∵面ABC的法向量
=(1,0,1),∵面ABC的法向量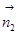 =(0,0,1),设二面角C1-AB-C的平面角为θ,∴cosθ=|cos<
=(0,0,1),设二面角C1-AB-C的平面角为θ,∴cosθ=|cos<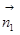 ,
,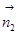 >|=
>|=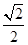 ,∴θ=45°,答案为45°.
,∴θ=45°,答案为45°.
考点:二面角的平面角
点评:本题考查二面角的平面角及求法,是基础题.解题时要认真审题,注意向量法的合理运用

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知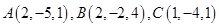 ,则向量
,则向量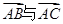 的夹角为 ( )
的夹角为 ( )
| A.30° | B.45° | C.60° | D.90° |
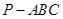 中,
中, 平面
平面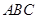 ,
,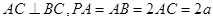 ,则
,则 与平面
与平面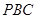 所成角的正弦值为__________.
所成角的正弦值为__________.
 ,且
,且 ∥
∥ ,则实数
,则实数 的值为 .
的值为 .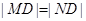 ,则点D的坐标为 .
,则点D的坐标为 .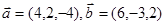 ,则
,则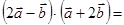 _______________.
_______________.