题目内容
20.已知定义在R上的函数f(x)满足:(1)f(x)+f(2-x)=0,(2)f(x-2)=f(-x),(3)在[-1,1]上表达式为f(x)=\left\{\begin{array}{l}\sqrt{1-{x^2}},x∈[-1,0]\\ cos(\frac{π}{2}x),x∈(0,1]\end{array},则函数f(x)与函数g(x)={2x,x≤01−x,x>0的图象区间[-3,3]上的交点个数为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 由题意可得函数f(x)的图象关于点M(1,0)对称,又关于直线x=-1对称;再结合g(x)的解析式画出这2个函数区间[-3,3]上的图象,数形结合可得它们的图象区间[-3,3]上的交点个数.
解答 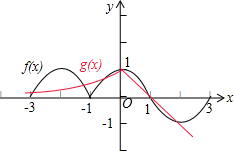 解:由f(x)+f(2-x)=0,可得函数f(x)的图象
解:由f(x)+f(2-x)=0,可得函数f(x)的图象
关于点M(1,0)对称.
由f(x-2)=f(-x),可得函数f(x)的图象
关于直线x=-1对称.
又f(x)在[-1,1]上表达式为
f(x)=\left\{\begin{array}{l}\sqrt{1-{x^2}},x∈[-1,0]\\ cos(\frac{π}{2}x),x∈(0,1]\end{array},
可得函数f(x)在[-3,3]上的图象以及函数g(x)={2x,x≤01−x,x>0在[-3,3]上的图象,
数形结合可得函数f(x)的图象与函数g(x)的图象区间[-3,3]上的交点个数为6,
故选:B.
点评 本题主要考查函数的图象的对称性,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.四面体ABCD的四个顶点均在半径为2的球面上,若AB、AC、AD两两垂直,→BA•→BC=2,则该四面体体积的最大值为( )
| A. | 7√26 | B. | 73 | C. | 2√2 | D. | 7√2 |
15.执行如图所示的程序框图,会输出一列数,则这个数列的第3项是( )


| A. | 870 | B. | 30 | C. | 6 | D. | 3 |
5.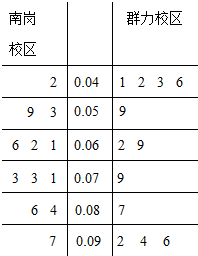 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )| A. | 南岗校区 | B. | 群力校区 | ||
| C. | 南岗、群力两个校区相等 | D. | 无法确定 |
12.已知复数z满足:zi=1+i(i是虚数单位),则z的虚部为( )
| A. | -i | B. | i | C. | 1 | D. | -1 |
7.若函数f(x)=(1-x2)(x2+ax+b)的图象关于直线x=2对称,则f(x)的最大值是( )
| A. | 9 | B. | 14 | C. | 15 | D. | 16 |