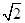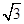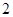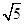题目内容
已知抛物线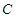 的顶点在坐标原点
的顶点在坐标原点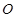 ,对称轴为
,对称轴为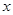 轴,焦点为
轴,焦点为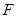 ,抛物线上一点
,抛物线上一点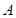 的横坐标为2,且
的横坐标为2,且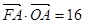 .
.
(1)求抛物线的方程;
(2)过点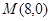 作直线
作直线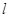 交抛物线于
交抛物线于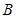 ,
,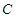 两点,求证:
两点,求证: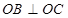 .
.
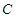 的顶点在坐标原点
的顶点在坐标原点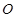 ,对称轴为
,对称轴为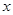 轴,焦点为
轴,焦点为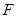 ,抛物线上一点
,抛物线上一点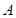 的横坐标为2,且
的横坐标为2,且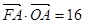 .
.(1)求抛物线的方程;
(2)过点
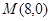 作直线
作直线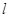 交抛物线于
交抛物线于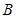 ,
,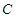 两点,求证:
两点,求证: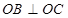 .
.(1)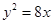 (2)详见解析.
(2)详见解析.
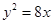 (2)详见解析.
(2)详见解析.试题分析:(1)可利用待定系数法设抛物线方程为
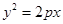
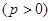 求解;
求解;(2)因为是直线与圆锥曲线的相交问,可以设直线方程(斜率不存在时单独讨论),然后联立抛物线方程和直线方程运用韦达定理结合条件来求解.
试题解析:解:(1)由题设抛物线的方程为:
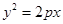
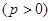 ,
,则点
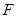 的坐标为
的坐标为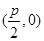 ,点
,点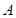 的一个坐标为
的一个坐标为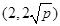 ,2分
,2分∵
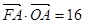 ,∴
,∴ ,4分
,4分∴
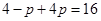 ,∴
,∴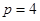 ,∴
,∴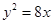 .6分
.6分(2)设
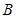 、
、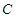 两点坐标分别为
两点坐标分别为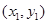 、
、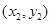 ,
,法一:因为直线当
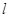 的斜率不为0,设直线当
的斜率不为0,设直线当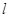 的方程为
的方程为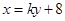
方程组
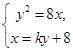 得
得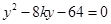 ,
,
因为
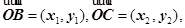
所以
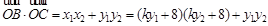
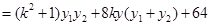 =0,
=0,所以
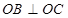 .
.法二:①当
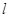 的斜率不存在时,
的斜率不存在时,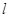 的方程为
的方程为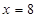 ,此时
,此时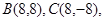
即
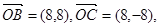 有
有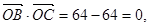 所以
所以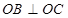 . 8分
. 8分当
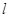 的斜率存在时,设
的斜率存在时,设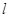 的方程为
的方程为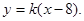
方程组
 得
得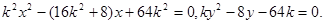
所以
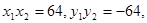 10分
10分因为
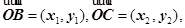
所以
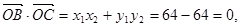
所以
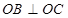 .
.由①②得
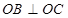 .12分
.12分
练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 :
: (
(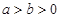 )的焦距为
)的焦距为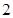 ,且过点(
,且过点(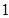 ,
,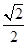 ),右焦点为
),右焦点为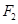 .设
.设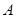 ,
,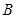 是
是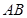 的中点
的中点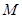 的横坐标为
的横坐标为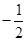 ,线段
,线段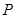 ,
,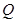 两点.
两点.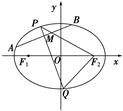
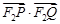 的取值范围.
的取值范围.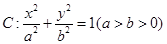 的离心率为
的离心率为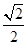 ,左右焦点分别为
,左右焦点分别为 ,且
,且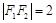 .
.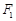 的直线与椭圆
的直线与椭圆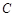 相交于
相交于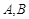 两点,且
两点,且 ,求
,求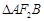 的面积.
的面积. 与椭圆
与椭圆 中心在原点,焦点均在
中心在原点,焦点均在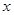 轴上,且离心率相同.椭圆
轴上,且离心率相同.椭圆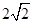 ,且椭圆
,且椭圆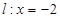 被椭圆
被椭圆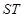 长为
长为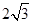 ,已知点
,已知点 是椭圆
是椭圆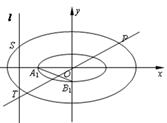
 为椭圆
为椭圆 为椭圆
为椭圆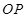 刚好平分
刚好平分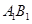 ,求点
,求点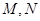 在椭圆
在椭圆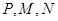 满足
满足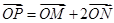 ,则直线
,则直线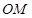 与直线
与直线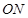 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.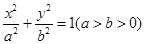 的左、右焦点分别为
的左、右焦点分别为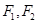 ,离心率为
,离心率为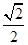 ,P是椭圆上一点,且
,P是椭圆上一点,且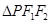 面积的最大值等于2.
面积的最大值等于2. 两焦点坐标分别为
两焦点坐标分别为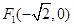 ,
,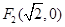 ,一个顶点为
,一个顶点为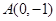 .
.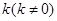 的直线
的直线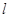 ,使直线
,使直线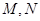 ,满足
,满足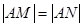 . 若存在,求出
. 若存在,求出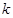 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.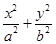 =1(a>b>0)的两个焦点F1,F2和上下两个顶点B1,B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点.
=1(a>b>0)的两个焦点F1,F2和上下两个顶点B1,B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点. 到两个定点
到两个定点 的距离之差的绝对值等于8,则动点M的轨迹方程为 ( )
的距离之差的绝对值等于8,则动点M的轨迹方程为 ( )



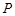 是双曲线
是双曲线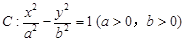 右支上一点,
右支上一点,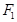 是双曲线的左焦点,且双曲线的一条渐近线恰是线段
是双曲线的左焦点,且双曲线的一条渐近线恰是线段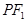 的中垂线,则该双曲线的离心率是( )
的中垂线,则该双曲线的离心率是( )