题目内容
已知函数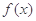 定义在区间
定义在区间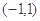 上,
上,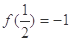 ,且当
,且当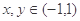 时,恒有
时,恒有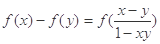 .又数列
.又数列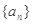 满足
满足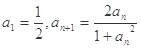 .
.
(Ⅰ)证明: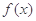 在
在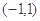 上是奇函数;
上是奇函数;
(Ⅱ)求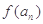 的表达式;
的表达式;
(III)设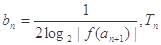 为数列
为数列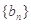 的前
的前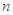 项和,若
项和,若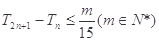 对
对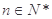 恒成立,求
恒成立,求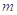 的最小值.
的最小值.
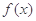 定义在区间
定义在区间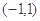 上,
上,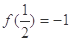 ,且当
,且当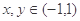 时,恒有
时,恒有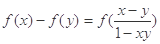 .又数列
.又数列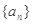 满足
满足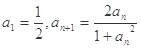 .
.(Ⅰ)证明:
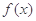 在
在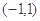 上是奇函数;
上是奇函数;(Ⅱ)求
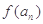 的表达式;
的表达式;(III)设
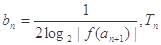 为数列
为数列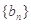 的前
的前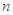 项和,若
项和,若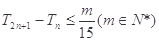 对
对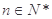 恒成立,求
恒成立,求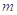 的最小值.
的最小值.(Ⅰ)见解析(Ⅱ)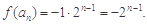 (III)m的最小值为7
(III)m的最小值为7
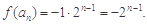 (III)m的最小值为7
(III)m的最小值为7本试题主要是考查了函数与数列的知识点的交汇处的运用。
(1)运用赋值法,令x=y=0时,则由已知有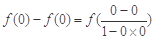 ,
,
可解得f (0)=0.
再令x=0,y∈(-1,1),则有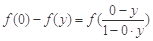 ,即
,即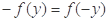 ,
,
∴ f (x)是(-1,1)上的奇函数
(2)令x=an,y= -an,于是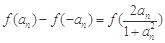 ,
,
由已知得2f (an)="f" (an+1),
∴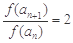 ,
,
从而得到 数列{f(an)}是以f(a1)=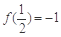 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
∴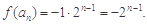
(3)由(II)得f(an+1)=-2n,于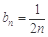 .
.
然后求解和式,得到结论。
解:(Ⅰ)证明:令x=y=0时,则由已知有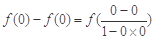 ,
,
可解得f (0)=0.
再令x=0,y∈(-1,1),则有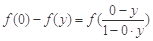 ,即
,即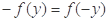 ,
,
∴ f (x)是(-1,1)上的奇函数. 4分
(Ⅱ)令x=an,y= -an,于是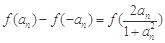 ,
,
由已知得2f (an)="f" (an+1),
∴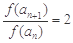 ,
,
∴ 数列{f(an)}是以f(a1)=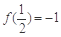 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
∴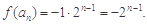 8分
8分
(III)由(II)得f(an+1)=-2n,于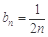 .
.
∴ Tn= b1+ b2+ b3+…+ bn
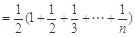 ,
,
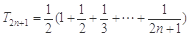 .
.
∴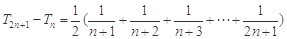 . 9分
. 9分
令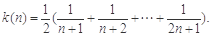
于是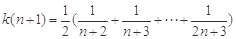 ,
,
∴ .
.
∴ k(n+1)<k(n),即k(n)在N*上单调递减, 12分
∴ k(n)max=k(1)=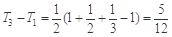 ,
,
∴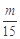 ≥
≥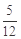 即m≥
即m≥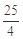 .
.
∵ m∈N*,
∴ m的最小值为7. 14分
(1)运用赋值法,令x=y=0时,则由已知有
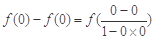 ,
,可解得f (0)=0.
再令x=0,y∈(-1,1),则有
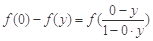 ,即
,即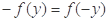 ,
,∴ f (x)是(-1,1)上的奇函数
(2)令x=an,y= -an,于是
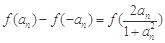 ,
,由已知得2f (an)="f" (an+1),
∴
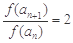 ,
,从而得到 数列{f(an)}是以f(a1)=
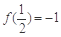 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.∴
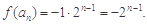
(3)由(II)得f(an+1)=-2n,于
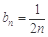 .
.然后求解和式,得到结论。
解:(Ⅰ)证明:令x=y=0时,则由已知有
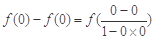 ,
,可解得f (0)=0.
再令x=0,y∈(-1,1),则有
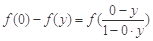 ,即
,即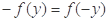 ,
,∴ f (x)是(-1,1)上的奇函数. 4分
(Ⅱ)令x=an,y= -an,于是
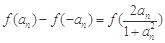 ,
,由已知得2f (an)="f" (an+1),
∴
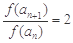 ,
,∴ 数列{f(an)}是以f(a1)=
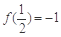 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.∴
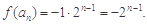 8分
8分(III)由(II)得f(an+1)=-2n,于
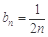 .
.∴ Tn= b1+ b2+ b3+…+ bn
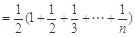 ,
,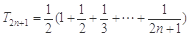 .
.∴
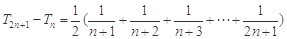 . 9分
. 9分令
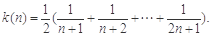
于是
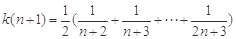 ,
,∴
 .
.∴ k(n+1)<k(n),即k(n)在N*上单调递减, 12分
∴ k(n)max=k(1)=
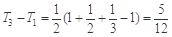 ,
,∴
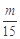 ≥
≥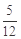 即m≥
即m≥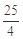 .
.∵ m∈N*,
∴ m的最小值为7. 14分

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
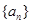 中,
中,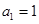 ,且点
,且点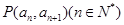 在直线
在直线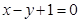 上.
上. 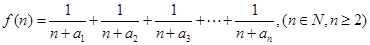 ,求证
,求证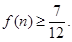
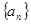 满足
满足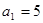 ,
,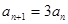 ,写出这个数列的前5项并归纳猜想通项公式。
,写出这个数列的前5项并归纳猜想通项公式。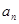 ﹜满足:
﹜满足: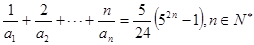 .(Ⅰ)求数列﹛
.(Ⅰ)求数列﹛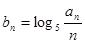 ,求
,求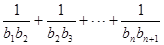
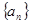 为等差数列,公差
为等差数列,公差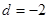 ,
,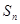 为其前
为其前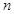 项和,若
项和,若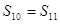 ,则
,则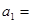 ( )
( )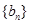 的前
的前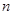 项和为
项和为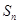 ,且
,且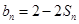 ;数列
;数列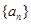 为等差数列,且
为等差数列,且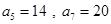 .
.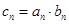 (
(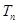 为数列
为数列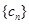 的前
的前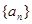 中,
中,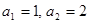 ,则数列
,则数列 的前
的前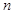 项和为
项和为 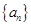 满足:
满足: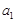 =
=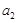 =2,
=2,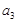 =3,
=3,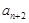 =
=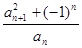 (
(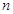 ≥2)
≥2)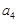 ,
,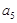 ,
,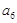 ;
;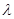 ,使得数列
,使得数列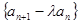 (
(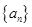 是公差不为零的等差数列,它的前
是公差不为零的等差数列,它的前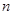 项和为
项和为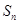 ,且
,且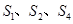 成等比数列,则
成等比数列,则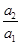 等于 ( )
等于 ( )