题目内容
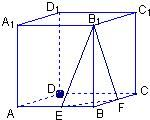18、在正方体ABCD-A1B1C1D1中，E，F分别是AB和BC的中点，试问在棱DD1上能否找到一点M，使BM⊥平面B1EF？若能，确定点M的位置；若不能，说明理由分析：B作BG⊥B1E交AA1于G，过G作GM∥AD交DD1于M，连BM，欲证BM⊥平面B1EF，根据直线与平面垂直的判定定理可知只需证BM与平面B1EF内两相交直线垂直，EF⊥BM，BM⊥B1E，EF∩B1E=E，满足定理要求．
解答：解：作法：①B作BG⊥B1E交AA1于G；
②过G作GM∥AD交DD1于M；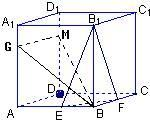
③连BM，则BM即为所求作
证明：连BD正方体ABCD-A1B1C1D1中，E，F为AB和BC的中点
∴BD⊥AC，又DD1⊥面ABCD∴EF⊥BM
又∵GM∥AD∴GM⊥面ABB1A1而BG⊥B1E∴BM⊥B1E
又EF∩B1E=E∴BM⊥平面B1EF
②过G作GM∥AD交DD1于M；
③连BM，则BM即为所求作
证明：连BD正方体ABCD-A1B1C1D1中，E，F为AB和BC的中点
∴BD⊥AC，又DD1⊥面ABCD∴EF⊥BM
又∵GM∥AD∴GM⊥面ABB1A1而BG⊥B1E∴BM⊥B1E
又EF∩B1E=E∴BM⊥平面B1EF
点评：本题主要考查了直线与平面垂直的性质，考查空间想象能力、运算能力和推理论证能力，属于中档题．
练习册系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）