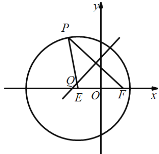
题目内容
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() ,右焦点到直线
,右焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)定义![]() 为
为![]() ,
,![]() 两点所在直线的斜率,若四边形
两点所在直线的斜率,若四边形![]() 为椭圆的内接四边形,且
为椭圆的内接四边形,且![]() ,
,![]() 相交于原点
相交于原点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)根据题意易得![]() 和
和![]() ,解出方程组即可得椭圆
,解出方程组即可得椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() ,易得
,易得![]() ,直线
,直线![]() 的方程为
的方程为![]() ,与椭圆方程联立与韦达定理相结合可得
,与椭圆方程联立与韦达定理相结合可得![]() ,根据对称性知
,根据对称性知![]() ,
,![]() 的斜率一个是
的斜率一个是![]() ,另一个就是
,另一个就是![]() ,故而可得结果.
,故而可得结果.
(1)解:设椭圆![]() :
:![]() 的半焦距为
的半焦距为![]() ,
,
因为椭圆![]() :
:![]() 经过点
经过点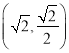 ,
,
所以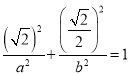 ,即
,即![]() ,
,
因为椭圆![]() 的右焦点到
的右焦点到![]() 的距离为
的距离为![]() ,所以
,所以![]() .
.
再由![]() 解得
解得![]() ,
,![]() ,
,![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)证明:设![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
设直线![]() 的方程为
的方程为![]() ,
,
联立![]() ,得
,得![]() ,
,
∴![]()
![]() ,
,
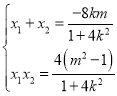 ,
,
∵![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() .
.
整理得![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,![]() 可以轮换,
可以轮换,
∴![]() ,
,![]() 的斜率一个是
的斜率一个是![]() ,另一个就是
,另一个就是![]() ,
,
∴![]()

【题目】中国武汉于2019年10月18日至2019年10月27日成功举办了第七届世界军人运动会.来自109个国家的9300余名运动员同台竞技.经过激烈的角逐,奖牌榜的前3名如下:
国家 | 金牌 | 银牌 | 铜牌 | 奖牌总数 |
中国 | 133 | 64 | 42 | 239 |
俄罗斯 | 51 | 53 | 57 | 161 |
巴西 | 21 | 31 | 36 | 88 |
某数学爱好者采用分层抽样的方式,从中国和巴西获得金牌选手中抽取了22名获奖代表.从这22名中随机抽取3人, 则这3人中中国选手恰好1人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】广东省2021年高考将实行“![]() ”模式,其最大特点就是取消文理科,除语文、数学、外语之外,从物理、历史这2科中自由选择一门科目;化学、生物、政治、地理这4科中自由选择两门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,从某学校高一年级的学生中随机抽取男生、女生个25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
”模式,其最大特点就是取消文理科,除语文、数学、外语之外,从物理、历史这2科中自由选择一门科目;化学、生物、政治、地理这4科中自由选择两门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,从某学校高一年级的学生中随机抽取男生、女生个25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
(1)请完成下面的![]() 列联表:
列联表:
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
(2)估计有多大把握认为选择全理与性别有关,并说明理由;
(3)现从这50名学生中已经选取了男生3名,女生2名进行座谈,从这5人中抽取2名代表作问卷调查,求至少抽到一名女生的概率.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:![]() ,其中
,其中![]() .
.