题目内容
某学校高一年学生在某次数学单元测试中,成绩在 的频数分布表如下:
的频数分布表如下:
(1)用分层抽样的方法从成绩在 ,
, 和
和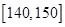 的同学中共抽取
的同学中共抽取 人,其中成绩在
人,其中成绩在 的有几人?
的有几人?
(2)从(1)中抽出的 人中,任取
人中,任取 人,求成绩在
人,求成绩在 和
和 中各有
中各有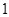 人的概率?
人的概率?
 的频数分布表如下:
的频数分布表如下:| 分数 |  | 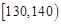 | 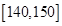 |
| 频数 | 60 | 20 | 20 |
(1)用分层抽样的方法从成绩在
 ,
, 和
和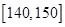 的同学中共抽取
的同学中共抽取 人,其中成绩在
人,其中成绩在 的有几人?
的有几人?(2)从(1)中抽出的
 人中,任取
人中,任取 人,求成绩在
人,求成绩在 和
和 中各有
中各有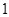 人的概率?
人的概率?(1)3人;(2)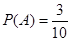
试题分析:(1)根据成绩在
 、
、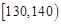 、
、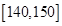 ]三组内的频数,计算出总人数然后根据分层抽样的定义即可得到结论;
]三组内的频数,计算出总人数然后根据分层抽样的定义即可得到结论;(2)从(1)中抽出的
 人中,成绩在
人中,成绩在 的有
的有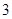 名同学,记为
名同学,记为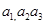 ,成绩在
,成绩在 和
和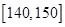 的各有1名同学,则从(1)中抽出的
的各有1名同学,则从(1)中抽出的 人中,列出任取
人中,列出任取 人的所有情况为10个,记事件
人的所有情况为10个,记事件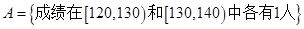 ,其包含的基本事件有
,其包含的基本事件有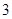 个,由古典概型即可求出
个,由古典概型即可求出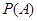 .
.(1)根据频数分布表,成绩在
 ,
, ,
,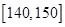 中共有
中共有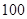 人,
人,成绩在
 的有
的有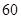 人,故用分层抽样的方法抽取成绩在
人,故用分层抽样的方法抽取成绩在 的人数为
的人数为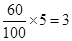 .
.(2)从(1)中抽出的
 人中,成绩在
人中,成绩在 的有
的有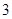 名同学,记为
名同学,记为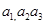 ,成绩在
,成绩在 和
和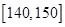 的各有1名同学,分别记为
的各有1名同学,分别记为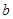 和
和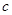 ,则从(1)中抽出的
,则从(1)中抽出的 人中,列出任取
人中,列出任取 人的所有情况为
人的所有情况为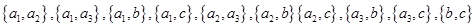 ,
,共有
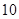 个基本事件,记事件
个基本事件,记事件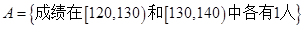 ,
,其包含的基本事件有
 个,分别是
个,分别是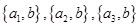 ,
, 故
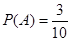 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 元/张
元/张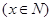 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少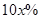 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少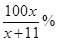 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?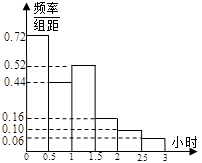
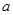 表示.
表示.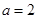 时,分别从甲,乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
时,分别从甲,乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.

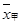 、
、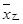 表示,则下列结论正确的是( )
表示,则下列结论正确的是( )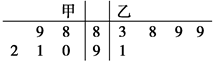
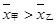 ,且甲比乙成绩稳定
,且甲比乙成绩稳定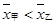 ,且甲比乙成绩稳定
,且甲比乙成绩稳定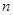 人,回答问题“皖江城市带有哪几个城市?”统计结果如图表所示:
人,回答问题“皖江城市带有哪几个城市?”统计结果如图表所示: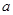
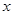
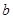
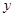
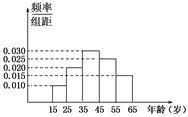
 的值;
的值;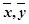 )
)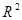 分别约为
分别约为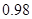 和
和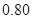 ,则模型乙的拟合效果更好
,则模型乙的拟合效果更好