题目内容
【题目】如图所示,平面内有三个向量 ![]() ,
, ![]() ,
, ![]() ,其中
,其中 ![]() 与
与 ![]() 的夹角为30°,
的夹角为30°, ![]() 与
与 ![]() 的夹角为90°,且|
的夹角为90°,且| ![]() |=2,|
|=2,| ![]() |=2,|
|=2,| ![]() |=2
|=2 ![]() ,若
,若 ![]() =λ
=λ ![]() +μ
+μ ![]() ,(λ,μ∈R)则( )
,(λ,μ∈R)则( ) 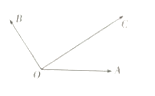
A.λ=4,μ=2
B.λ=4,μ=1
C.λ=2,μ=1
D.λ=2,μ=2
【答案】C
【解析】解:过点C作CE∥OB交OA的延长线于点E,过点C作CF∥OA交OB的延长线于点F,则 ![]() =
= ![]() +
+ ![]() .
.

∴∠OCE=∠COF=90°,∵∠COE=30°,∴CE= ![]() OE,
OE,
∵CE2+OC2=OE2,
∴CE=2,OE=4.
∵OA=2, ![]() =λ
=λ ![]() +μ
+μ ![]() ,(λ,μ∈R).
,(λ,μ∈R).
∴λ= ![]() =2,μ=
=2,μ= ![]() =
= ![]() =1,
=1,
故选:C
【考点精析】本题主要考查了平面向量的基本定理及其意义的相关知识点,需要掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目