题目内容
【题目】(本小题满分12分)已知椭圆C: ![]() 的离心率为
的离心率为![]() ,右焦点为(
,右焦点为(![]() ,0).(1)求椭圆C的方程;(2)若过原点
,0).(1)求椭圆C的方程;(2)若过原点![]() 作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值.
作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值.
【答案】(1) ![]() ,(2) O到直线
,(2) O到直线![]() 的距离为定值
的距离为定值![]() .
.
【解析】试题分析:(1)根据焦点和离心率列方程解出a,b,c;
(2)对于AB有无斜率进行讨论,设出A,B坐标和直线方程,利用根与系数的关系和距离公式计算;
试题解析:(1)由右焦点为(![]() ,0),则
,0),则![]() ,又离心率为
,又离心率为![]() ,所以
,所以![]() ,
, ![]() ,
,
则 ![]()
(2) 设![]() ,
, ![]() ,若k存在,则设直线AB:y=kx+m.
,若k存在,则设直线AB:y=kx+m. ![]()
得![]()
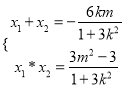
有OA⊥OB知x1x2+y1y2=x1x2+(k x1+m) (k x2+m)=(1+k2) x1x2+k m(x1+x2)=0 代入,得4 m2=3 k2+3原点到直线AB的距离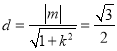 , 当AB的斜率不存在时,
, 当AB的斜率不存在时, ![]() ,可得,
,可得, ![]() 依然成立.所以点O到直线
依然成立.所以点O到直线![]() 的距离为定值
的距离为定值![]() .
.

【题目】心理学家分析发现“喜欢空间想象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按分层抽样的方法抽取50名同学(男生30人、女生20人),给每位同学立体几何题、代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如下表:(单位:人)
立体几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(2)经统计得,选择做立体几何题的学生正答率为![]() ,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()