题目内容
已知数列{an}、{bn}满足 bn=
bn=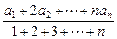 ,求证:数列{an}成等差数列的充要条件是数列{bn}也是等差数列。
,求证:数列{an}成等差数列的充要条件是数列{bn}也是等差数列。

 bn=
bn=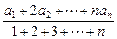 ,求证:数列{an}成等差数列的充要条件是数列{bn}也是等差数列。
,求证:数列{an}成等差数列的充要条件是数列{bn}也是等差数列。
证明略
①必要性:
设{an}成等差数列,公差为d,∵{an}成等差数列
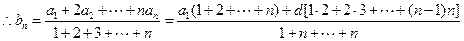
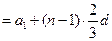
从而bn+1-bn=a1+n·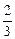 d-a1-(n-1)
d-a1-(n-1)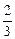 d=
d=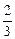 d为常数。
d为常数。
故{bn}是等差数列,公差为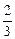 d。
d。
②充分性:
设{bn}是等差数列,公差为d′,则bn=(n-1)d′
∵bn(1+2+…+n)=a1+2a2+…+nan ①
bn-1(1+2+…+n-1)=a1+2a2+…+(n-1)an ②
①-②得:nan=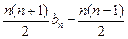 bn-1?
bn-1?
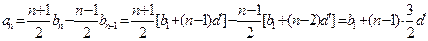
从而得an+1-an=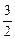 d′为常数,故{an}是等差数列。
d′为常数,故{an}是等差数列。
综上所述,数列{an}成等差数列的充要条件是数列{bn}也是等差数列。
设{an}成等差数列,公差为d,∵{an}成等差数列

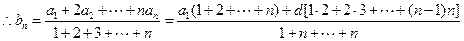
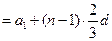
从而bn+1-bn=a1+n·
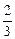 d-a1-(n-1)
d-a1-(n-1)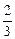 d=
d=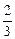 d为常数。
d为常数。故{bn}是等差数列,公差为
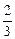 d。
d。②充分性:
设{bn}是等差数列,公差为d′,则bn=(n-1)d′
∵bn(1+2+…+n)=a1+2a2+…+nan ①
bn-1(1+2+…+n-1)=a1+2a2+…+(n-1)an ②
①-②得:nan=
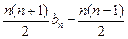 bn-1?
bn-1?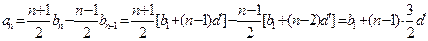
从而得an+1-an=
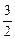 d′为常数,故{an}是等差数列。
d′为常数,故{an}是等差数列。综上所述,数列{an}成等差数列的充要条件是数列{bn}也是等差数列。

练习册系列答案
相关题目
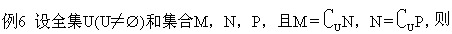
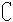 UP B.M=P
UP B.M=P
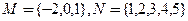 ,映射
,映射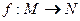 使得对任意的
使得对任意的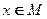 ,都有
,都有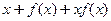 是奇数,则这样的映射
是奇数,则这样的映射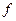 的个数是 ( )
的个数是 ( )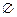 ,求实数m的取值范围.
,求实数m的取值范围.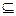 B,试求k的取值范围.
B,试求k的取值范围.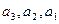 ,若满足
,若满足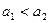 ,
,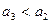 ,则称该三位数为凸数,则所有的凸数有_____________个。
,则称该三位数为凸数,则所有的凸数有_____________个。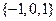 的所有子集个数为
的所有子集个数为 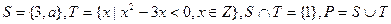 ,那么集合P的子集个数是 ( )
,那么集合P的子集个数是 ( )