题目内容
设甲、乙、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.三人各向目标射击一次,求至少有一人命中目标的概率及恰有两人命中目标的概率.
0.94 0.44
解析解:设Ak表示“第k人命中目标”,k=1,2,3.
这里,A1,A2,A3独立,且P(A1)=0.7,P(A2)=0.6,P(A3)=0.5.
从而,至少有一人命中目标的概率为1-P( 1·
1· 2·
2· 3)=1-P(
3)=1-P( 1)P(
1)P( 2)P(
2)P( 3)=1-0.3×0.4×0.5=0.94.
3)=1-0.3×0.4×0.5=0.94.
恰有两人命中目标的概率为
P(A1·A2· 3+A1·
3+A1· 2·A3+
2·A3+ 1·A2·A3)
1·A2·A3)
=P(A1·A2· 3)+P(A1·
3)+P(A1· 2·A3)+P(
2·A3)+P( 1·A2·A3)
1·A2·A3)
=P(A1)P(A2)P( 3)+P(A1)P(
3)+P(A1)P( 2)P(A3)+
2)P(A3)+
P( 1)P(A2)P(A3)=0.7×0.6×0.5+0.7×0.4×0.5+0.3×0.6×0.5=0.44.
1)P(A2)P(A3)=0.7×0.6×0.5+0.7×0.4×0.5+0.3×0.6×0.5=0.44.
∴至少有一人命中目标的概率为0.94,恰有两人命中目标的概率为0.44.

练习册系列答案
相关题目
甲、乙两药厂生产同一型号药品,在某次质量检测中,两厂各有5份样品送检,检测的平均得分相等(检测满分为100分,得分高低反映该样品综合质量的高低).成绩统计用茎叶图表示如下:
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 |  6 6 |
(1)求
 ;
;(2)某医院计划采购一批该型号药品,从质量的稳定性角度考虑,你认为采购哪个药厂的产品
比较合适?
(3)检测单位从甲厂送检的样品中任取两份作进一步分析,在抽取的两份样品中,求至少有一份得分在(90,100]之间的概率.
对一批共50件的某电器进行分类检测,其重量(克)统计如下:
| 重量段 | [80,85) | [85,90) | [90,95) | [95,100] |
| 件数 | 5 | a | 15 | b |
(1)从该批电器中任选1件,求其为“B”型的概率;
(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率.

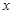 (
( ≥0)万元,投资B项目资金为
≥0)万元,投资B项目资金为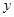 (
(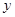 ≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利
≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利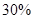 的可能性为
的可能性为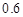 ,亏损
,亏损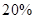 的可能性为
的可能性为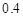 ;位于二类风区的B项目获利
;位于二类风区的B项目获利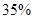 的可能性为
的可能性为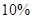 的可能性是
的可能性是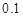 ,不赔不赚的可能性是
,不赔不赚的可能性是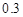 .
. 和
和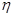 ,试写出随机变量
,试写出随机变量 ,
,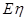 ;
;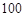 万元的资金投资于A,B项目,且公司要求对A项目的投
万元的资金投资于A,B项目,且公司要求对A项目的投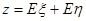 的最大值.
的最大值. ;
; ;
; ;
; 个等式并证明;
个等式并证明;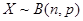 ,求证:
,求证: .
. ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .
.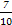 ,并指出袋中哪种颜色的球的个数最少.
,并指出袋中哪种颜色的球的个数最少.