题目内容
有驱虫药1618和1573各3杯,从中随机取出3杯称为一次试验(假定每杯被取到的概率相等),将1618全部取出称为试验成功.
(1)求恰好在第3次试验成功的概率(要求将结果化为最简分数).
(2)若试验成功的期望值是2,需要进行多少次相互独立重复试验?
(1)试验一次就成功的概率为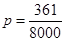 ; (2)4.
; (2)4.
解析试题分析:(1) 从6杯中任选3杯,不同选法共有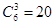 种,而选到的3杯都是1618的选法只有1种,由古典概型概率的求法可得试验一次就成功的概率为
种,而选到的3杯都是1618的选法只有1种,由古典概型概率的求法可得试验一次就成功的概率为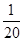 .恰好在第3次试验成功相当于前两次试验都没成功,第3次才成功.由于成功的概率为
.恰好在第3次试验成功相当于前两次试验都没成功,第3次才成功.由于成功的概率为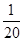 ,所以一次试验没有成功的概率为
,所以一次试验没有成功的概率为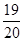 ,三次相乘即得所求概率.(2)该例是一个二项分布,二项分布的期望是
,三次相乘即得所求概率.(2)该例是一个二项分布,二项分布的期望是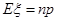 ,解此方程即可得次数
,解此方程即可得次数 .
.
试题解析:(1)从6杯中任选3杯,不同选法共有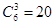 种,而选到的3杯都是1618的选法只有1种,从而试验一次就成功的概率为
种,而选到的3杯都是1618的选法只有1种,从而试验一次就成功的概率为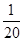 .恰好在第3次试验成功相相当于前两次试验都没成功,第3次才成功,故概率为
.恰好在第3次试验成功相相当于前两次试验都没成功,第3次才成功,故概率为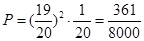 .
.
(2)假设连续试验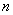 次,则试验成功次数
次,则试验成功次数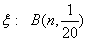 ,从而其期望为
,从而其期望为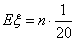 ,再由
,再由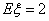 可解出
可解出 .
.
考点:1、古典概型;2、二项分布及其期望.

练习册系列答案
相关题目
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
(1)假设n=4,在第一大块地中,种植品种甲的小块地的数目记为X,求X的分布列和数学期望;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
| 品种甲 | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| 品种乙 | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表:
| 评估的平均得分 | 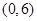 | 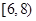 | 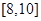 |
| 全市的总体交通状况等级 | 不合格 | 合格 | 优秀 |
(2)用简单随机抽样方法从这
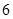 条道路中抽取
条道路中抽取 条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过
条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过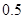 的概率.
的概率. 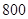 名男生中随机抽取
名男生中随机抽取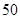 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于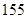 cm和
cm和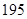 cm之间,将测量结果按如下方式分成八组:第一组[
cm之间,将测量结果按如下方式分成八组:第一组[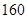 ),第二组[
),第二组[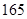 ),…,第八组[
),…,第八组[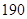 ,
,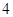 人.
人.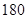 cm以上(含
cm以上(含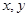 ,事件
,事件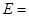 {
{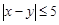 },求
},求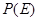 .
.
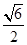 .
.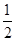 ,乙、丙应聘成功的概率均为
,乙、丙应聘成功的概率均为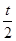 ,(0<t<2),且三个人是否应聘成功是相互独立的.
,(0<t<2),且三个人是否应聘成功是相互独立的.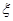 ,若当且仅当为
,若当且仅当为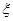 表示开始第4次发球时乙的得分,求
表示开始第4次发球时乙的得分,求