题目内容
20．2015年8月6日凌晨，马来西亚总理纳吉布在吉隆坡确认，7月29日在法属留尼汪岛发现的飞机残骸来自515天前失联的马航MH370．若一架侦察机以500米/秒的速度在留尼汪岛上空平行于地面匀速飞行时，发现飞机残骸在侦察机前方且俯角为30°的地面上，半分钟后，侦察机发现飞机残骸仍在其前方且俯角为75°的地面上，则侦察机的飞行高度是3750（1+$\sqrt{3}$）米（保留根号）分析 如图所示，AB=15000米，∠A=30°，∠C=75°-30°=45°，B=105°，由正弦定理可得AC，即可求出侦察机的飞行高度．
解答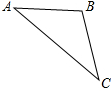 
解：如图所示，由题意得，AB=15000米，∠A=30°，∠C=75°-30°=45°，∴B=105°，
∴由正弦定理可得$\frac{15000}{sin45°}=\frac{AC}{sin105°}$，∴AC=7500（1+$\sqrt{3}$）
∴侦察机的飞行高度是ACsin30°=3750（1+$\sqrt{3}$）．
故答案为：3750（1+$\sqrt{3}$）
点评 本题考查利用数学知识解决实际问题，考查正弦定理的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
5．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的右焦点F到渐近线和直线$x=\frac{a^2}{c}$的距离之比为2：1，则双曲线的渐近线方程为（ ）
| A． | y=±$\frac{\sqrt{3}}{3}$x | B． | y=±$\sqrt{2}$x | C． | y=±$\sqrt{3}$x | D． | y=±2x |