题目内容
已知函数 其中a是实数.设
其中a是实数.设 ,
, 为该函数图象上的两点,且
为该函数图象上的两点,且 .
.
(1)指出函数f(x)的单调区间;
(2)若函数f(x)的图象在点A,B处的切线互相垂直,且 ,求
,求 的最小值;
的最小值;
(3)若函数f(x)的图象在点A,B处的切线重合,求a的取值范围.
 其中a是实数.设
其中a是实数.设 ,
, 为该函数图象上的两点,且
为该函数图象上的两点,且 .
.(1)指出函数f(x)的单调区间;
(2)若函数f(x)的图象在点A,B处的切线互相垂直,且
 ,求
,求 的最小值;
的最小值;(3)若函数f(x)的图象在点A,B处的切线重合,求a的取值范围.
(1)[-1,0),(0,+∞)
(2)1
(3)(-ln2-1,+∞)
(2)1
(3)(-ln2-1,+∞)
(1)函数f(x)的单调递减区间为(-∞,-1),单调递增区间为[-1,0),(0,+∞).
(2)由导数的几何意义可知,点A处的切线斜率为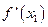 ,点B处的切线斜率为
,点B处的切线斜率为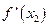 ,
,
故当点A处的切线与点B处的切线垂直时,有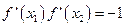 .
.
当x<0时,对函数f(x)求导,得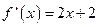 .
.
因为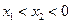 ,所以
,所以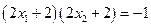 ,
,
所以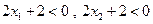 .
.
因此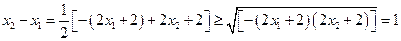
当且仅当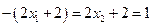 ,即
,即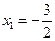 且
且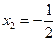 时等号成立.
时等号成立.
所以函数f(x)的图象在点A,B处的切线互相垂直时, 的最小值为1.
的最小值为1.
(3)当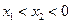 或
或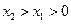 时,
时,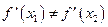 ,故
,故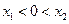 .
.
当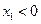 时,函数f(x)的图象在点
时,函数f(x)的图象在点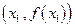 处的切线方程为
处的切线方程为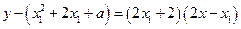 ,
,
即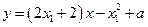 .
.
当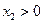 时,函数f(x)的图象在点
时,函数f(x)的图象在点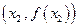 处的切线方程为
处的切线方程为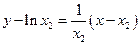 ,即
,即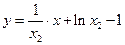 .
.
两切线重合的充要条件是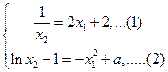
由(1)式及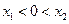 知,
知,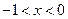 .
.
由(1)(2)式得,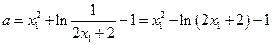 .
.
设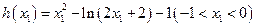 ,
,
则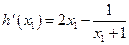 .
.
所以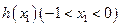 是减函数.
是减函数.
则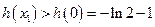 .
.
所以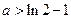 .
.
又当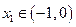 且趋近于-1时,
且趋近于-1时,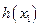 无限增大,
无限增大,
所以a的取值范围是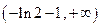 .
.
故当函数f(x)的图象在点A,B处的切线重合时,a的取值范围是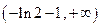 .
.
(2)由导数的几何意义可知,点A处的切线斜率为
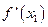 ,点B处的切线斜率为
,点B处的切线斜率为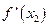 ,
,故当点A处的切线与点B处的切线垂直时,有
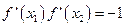 .
.当x<0时,对函数f(x)求导,得
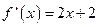 .
.因为
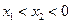 ,所以
,所以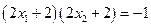 ,
,所以
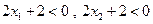 .
.因此
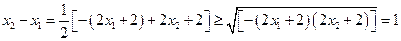
当且仅当
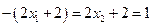 ,即
,即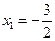 且
且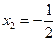 时等号成立.
时等号成立.所以函数f(x)的图象在点A,B处的切线互相垂直时,
 的最小值为1.
的最小值为1.(3)当
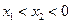 或
或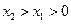 时,
时,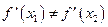 ,故
,故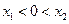 .
.当
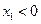 时,函数f(x)的图象在点
时,函数f(x)的图象在点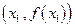 处的切线方程为
处的切线方程为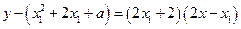 ,
,即
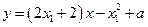 .
.当
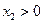 时,函数f(x)的图象在点
时,函数f(x)的图象在点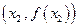 处的切线方程为
处的切线方程为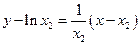 ,即
,即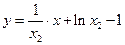 .
.两切线重合的充要条件是
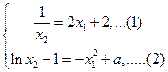
由(1)式及
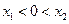 知,
知,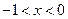 .
.由(1)(2)式得,
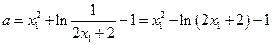 .
.设
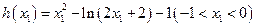 ,
,则
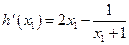 .
.所以
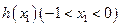 是减函数.
是减函数.则
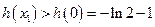 .
.所以
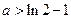 .
.又当
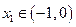 且趋近于-1时,
且趋近于-1时,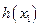 无限增大,
无限增大,所以a的取值范围是
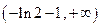 .
.故当函数f(x)的图象在点A,B处的切线重合时,a的取值范围是
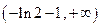 .
.
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
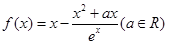 .
. 时,证明:当
时,证明:当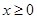 时,
时,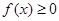 ;
;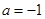 时,证明:
时,证明: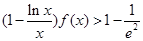 .
.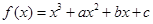 在
在 与
与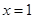 时都取得极值
时都取得极值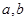 的值与函数
的值与函数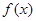 的单调区间
的单调区间 ,不等式
,不等式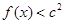 恒成立,求
恒成立,求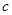 的取值范围
的取值范围 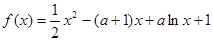
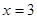 是
是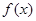 的极值点,求
的极值点,求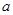 的范围,使得
的范围,使得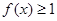 恒成立.
恒成立.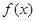 是定义在R上的奇函数,且
是定义在R上的奇函数,且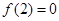 ,当x>0时,有
,当x>0时,有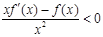 恒成立,则不等式
恒成立,则不等式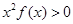 的解集是 ( )
的解集是 ( )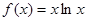 ,当
,当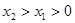 时,给出下列几个结论:
时,给出下列几个结论: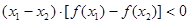 ;②
;②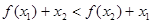 ;③
;③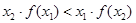 ;
;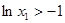 时,
时,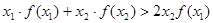 .
.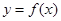 的导函数
的导函数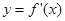 的图象,给出下列命题:
的图象,给出下列命题: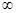 ,-2)上单调递减
,-2)上单调递减
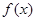 是定义在
是定义在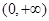 上的非负可导函数,且满足
上的非负可导函数,且满足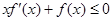 ,对任意正数
,对任意正数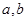 ,若
,若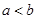 ,则必有( )
,则必有( )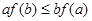
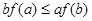
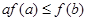
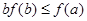
 的定义域为开区间
的定义域为开区间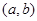 ,导函数
,导函数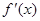 在
在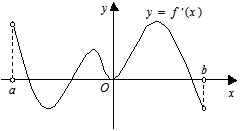
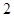 个
个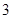 个
个 个
个