题目内容
给出下列四个命题:①用cardA表示有限集A的元素个数,则A⊆B?cardA≤cardB;②函数f(x)满足对任意x都有f(x+3)=f(x-3)?f(x)的图象关于直线x=3对称;
③在△ABC中,A,B,C为三个内角,则A>B?cos2A<cos2B;
④λ1,λ2,t1,t2为实数,若
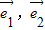 不共线,则
不共线,则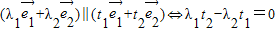 .
.其中正确命题的个数有( )
A.1个
B.2个
C.3个
D.4个
【答案】分析:根据集合子集的定义及性质,我们可以判断①的真假,
根据函数的周期性,我们可以判断②的真假,
根据正弦定理,及同角三角函数的基本关系,我们可以判断③的真假,
根据向量共线的充要条件,我们可以判断出④的真假,进而得到答案.
解答:解:根据集合子集的定义,我们易得当A⊆B⇒cardA≤cardB,但当cardA≤cardB时,A⊆B不一定成立,故①错误;
根据函数的周期性,可得对任意x都有f(x+3)=f(x-3)?f(x)中周期为6的周期函数,故②错误;
在△ABC中,A,B,C为三个内角,则A>B?sinA>sinB?sin2A>sin2B?1-cos2A>1-cos2B?cos2A<cos2B,故③正确;
λ1,λ2,t1,t2为实数,若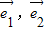 不共线,根据向量共线的充要条件,可得
不共线,根据向量共线的充要条件,可得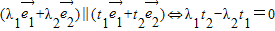 ,故④正确;
,故④正确;
故选B
点评:本题考查的知识点是元素与集合关系的判断,函数的周期性,平面向量的基本定理及其意义,正弦定理,同角三角函数的基本关系,其中根据上述基本知识点,判断题目中四个命题的真假,是解答本题的关键.
根据函数的周期性,我们可以判断②的真假,
根据正弦定理,及同角三角函数的基本关系,我们可以判断③的真假,
根据向量共线的充要条件,我们可以判断出④的真假,进而得到答案.
解答:解:根据集合子集的定义,我们易得当A⊆B⇒cardA≤cardB,但当cardA≤cardB时,A⊆B不一定成立,故①错误;
根据函数的周期性,可得对任意x都有f(x+3)=f(x-3)?f(x)中周期为6的周期函数,故②错误;
在△ABC中,A,B,C为三个内角,则A>B?sinA>sinB?sin2A>sin2B?1-cos2A>1-cos2B?cos2A<cos2B,故③正确;
λ1,λ2,t1,t2为实数,若
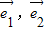 不共线,根据向量共线的充要条件,可得
不共线,根据向量共线的充要条件,可得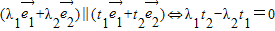 ,故④正确;
,故④正确;故选B
点评:本题考查的知识点是元素与集合关系的判断,函数的周期性,平面向量的基本定理及其意义,正弦定理,同角三角函数的基本关系,其中根据上述基本知识点,判断题目中四个命题的真假,是解答本题的关键.

练习册系列答案
相关题目