题目内容
8.在△ABC中,∠ABC=120°,BA=2,BC=3,D,E是线段AC的三等分点,则$\overrightarrow{BD}$•$\overrightarrow{BE}$的值为$\frac{11}{9}$.分析 根据向量加法、减法的几何意义,可用$\overrightarrow{BA},\overrightarrow{BC}$分别表示$\overrightarrow{BD},\overrightarrow{BE}$,从而进行数量积的运算即可.
解答 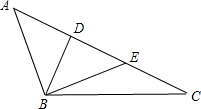 解:如图,
解:如图,
根据已知条件:
$\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}$=$\overrightarrow{BA}+\frac{1}{3}\overrightarrow{AC}=\overrightarrow{BA}+\frac{1}{3}(\overrightarrow{BC}-\overrightarrow{BA})$=$\frac{1}{3}(2\overrightarrow{BA}+\overrightarrow{BC})$;
同理$\overrightarrow{BE}=\frac{1}{3}(\overrightarrow{BA}+2\overrightarrow{BC})$;
∴$\overrightarrow{BD}•\overrightarrow{BE}=\frac{1}{9}(2{\overrightarrow{BA}}^{2}+5\overrightarrow{BA}•\overrightarrow{BC}+2{\overrightarrow{BC}}^{2})$=$\frac{1}{9}(8-15+18)=\frac{11}{9}$.
故答案为:$\frac{11}{9}$.
点评 考查向量加法、减法的几何意义,线段三等分点的定义,以及向量计算公式及运算.

练习册系列答案
相关题目
19. 已知MOD函数是一个求余数的函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入n=25时,则输出的结果为( )
已知MOD函数是一个求余数的函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入n=25时,则输出的结果为( )
 已知MOD函数是一个求余数的函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入n=25时,则输出的结果为( )
已知MOD函数是一个求余数的函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.如图是一个算法的程序框图,当输入n=25时,则输出的结果为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
3.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下:
则该营业窗口上午9点钟时,至少有2人排队的概率是0.74.
| 排队人数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
20.某女士为将体重维持在正常水平,每天坚持体育锻炼.已知该女士某星期一测得其体重是50kg,而后每天测得的体重与前一天相比,或减少0.5kg或维持不变或增加0.5kg,若该星期天该女士测得其体重仍然是50kg,则该女士在这个星期内每天测得的体重的所有可能结果有( )
| A. | 121种 | B. | 141种 | C. | 231种 | D. | 282种 |
17.已知$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个顶点和一个焦点在圆x2+y2-x-y-6=0上,则双曲线的虚轴长为( )
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{5}$ |
