Question

设F₁、F₂是双曲线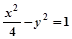的两个焦点，P在双曲线上，且满足∠F₁PF₂=90°，则△PF₁F₂的面积是(    )

A．1                B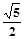．              C．2                D．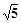

 

Answer 1

【答案】

A

【解析】

试题分析：设|PF₁|=x，|PF₂|=y，根据根据双曲线性质可知x-y的值，再根据∠F₁PF₂=90°，求得x²+y²的值，进而根据2xy=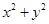 -（x-y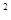）求得xy，进而可求得∴△F₁PF₂的面积. 解：设|PF₁|=x，|PF₂|=y，（x＞y），根据双曲线性质可知x-y=4，∵∠F₁PF₂=90°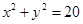，∴，∴2xy=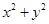-（x-y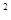）=4，∴xy=2，∴△F₁PF₂的面积为 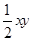=1，故选A

考点：双曲线的简单性质

点评：本题主要考查了双曲线的简单性质．要灵活运用双曲线的定义及焦距、实轴、虚轴等之间的关