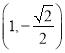Question

【题目】已知E、F分别在正方体ABCD﹣A1B1C1D1的棱BB1、CC1上，且B1E=2EB，CF=2FC1 ， 则面AEF与面ABC所成的二面角的正切值等于 ．

Answer 1

【答案】
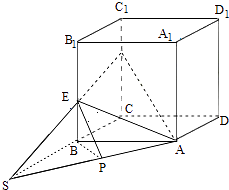
【解析】解：由题意画出图形如图：
因为E、F分别在正方体ABCD﹣A1B1C1D1的棱BB1、CC1上，且B1E=2EB，CF=2FC1 ，
延长CB、FE交点为S连接AS，过B作BP⊥AS连接PE，所以面AEF与面ABC所成的二面角就是∠BPE，因为B1E=2EB，CF=2FC1 ，
所以BE：CF=1：2
所以SB：SC=1：2，
设正方体的棱长为：a，所以AS= a，BP= a，BE= ，在RT△PBE中，tan∠EPB= = = ，
所以答案是：