题目内容
【题目】如图,双曲线![]() 的两顶点为
的两顶点为![]() ,
,![]() ,虚轴两端点为
,虚轴两端点为![]() ,
,![]() ,两焦点为
,两焦点为![]() ,
,![]() ,若以
,若以![]() 为直径的圆内切于菱形
为直径的圆内切于菱形![]() ,切点分别为
,切点分别为![]() ,
,![]() ,
,![]() ,
,![]() .则
.则
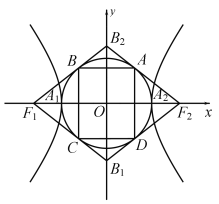
(1)双曲线的离心率![]() ______;
______;
(2)菱形![]() 的面积
的面积![]() 与矩形
与矩形![]() 的面积
的面积![]() 的比值
的比值![]() ______.
______.
【答案】![]() .
. ![]() .
.
【解析】
对于(1)由题意可得顶点和虚轴端点坐标及交点坐标,从而求得菱形的边长,得到![]() 到直线的距离为
到直线的距离为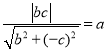 ,接下来根据双曲线中
,接下来根据双曲线中![]() 的关系和离心率公式,即可得到所求值;对于(2),分别计算出菱形
的关系和离心率公式,即可得到所求值;对于(2),分别计算出菱形![]() 面积
面积![]() 与矩形
与矩形![]() 的面积
的面积![]() ,然后根据
,然后根据![]() 的关系求出它们的比值即可.
的关系求出它们的比值即可.
(1)直线![]() 的方程为
的方程为![]() ,
,
所以![]() 到直线的距离为
到直线的距离为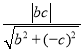 ,
,
因为以![]() 为直径的圆内切于菱形
为直径的圆内切于菱形![]() ,
,
所以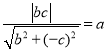 ,
,
所以![]() ,
,
所以![]() ,即
,即![]() ,
,
因为![]() ,解得
,解得![]() ,
,![]() ,
,
故答案为:![]() .
.
(2)菱形![]() 的面积
的面积![]() ,
,
设矩形![]() ,
,![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以矩形![]() 的面积
的面积![]() ,
,
所以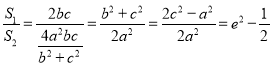 ,
,
由(1)知![]() ,所以
,所以![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】一饮料店制作了一款新饮料,为了进行合理定价先进行试销售,其单价![]() (元)与销量
(元)与销量![]() (杯)的相关数据如下表:
(杯)的相关数据如下表:
单价 | 8.5 | 9 | 9.5 | 10 | 10.5 |
销量 | 120 | 110 | 90 | 70 | 60 |
(1)已知销量![]() 与单价
与单价![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该款新饮料每杯的成本为8元,试销售结束后,请利用(1)所求的线性回归方程确定单价定为多少元时,销售的利润最大?(结果四舍五入保留到整数)
附:线性回归方程![]() 中斜率和截距最小二乗法估计计算公式:
中斜率和截距最小二乗法估计计算公式: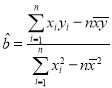 ,
,![]() ,
,![]() ,
,![]() .
.