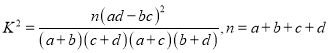题目内容
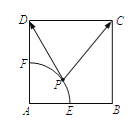
【题目】如图所示,平面多边形![]() 中,AE=ED,AB=BD,且
中,AE=ED,AB=BD,且![]() ,现沿直线
,现沿直线![]() ,将
,将![]() 折起,得到四棱锥
折起,得到四棱锥![]() .
.

(1)求证: ![]() ;
;
(2)若![]() ,求PD与平面
,求PD与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)正弦值为![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连
,连![]() ,由题意可得
,由题意可得![]() 且
且![]() ,则有
,则有![]() 平面
平面![]() ,可得结论;(2)法一:以O为坐标原点,OB, OD, OP所在的直线为x,y,z轴建立空间直角坐标系,求出平面PAB的一个法向量,再利用向量的夹角公式求解即可;法二:利用等积法:由
,可得结论;(2)法一:以O为坐标原点,OB, OD, OP所在的直线为x,y,z轴建立空间直角坐标系,求出平面PAB的一个法向量,再利用向量的夹角公式求解即可;法二:利用等积法:由![]() 得
得![]() =
= ![]() ,求出点D到平面PAB的距离为h
,求出点D到平面PAB的距离为h![]() ,设PD与平面
,设PD与平面![]() 所成角为
所成角为![]() ,则
,则![]() =
=![]() =
=![]() =
=![]() .
.
解析:
(1)证明:取![]() 的中点
的中点![]() ,连
,连![]() ,
,

∵![]() ,即
,即![]() ,
,
∴![]() 且
且![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,
,
∴![]() .
.
(2)∵OP=1,OB=2,
![]() ,
,
∴![]() ,
,
∴OP、OB、OD两两互相垂直,
以O为坐标原点,OB, OD, OP所在的直线为x,y,z轴建立如图所示空间直角坐标系,
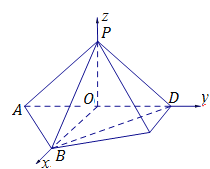
则![]() ,
,
![]() ,
,
设![]() 为平面PAB的一个法向量,则
为平面PAB的一个法向量,则
由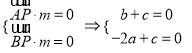 ,
,
令![]() 则得
则得![]() ,
,
∴![]() ,
,
设PD与平面![]() 所成角为
所成角为![]() ,
,
则![]() =
=![]() =
=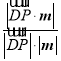 =
=![]() =
=![]() ,
,
故![]() ,
,
即PD与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】微信支付诞生于微信红包,早期知识作为社交的一部分“发红包”而诞生的,在发红包之余才发现,原来微信支付不仅可以用来发红包,还可以用来支付,现在微信支付被越来越多的人们所接受,现从某市市民中随机抽取300为对是否使用微信支付进行调查,得到下列![]() 的列联表:
的列联表:
年轻人 | 非年轻人 | 总计 | |
经常使用微信支付 | 165 | 225 | |
不常使用微信支付 | |||
合计 | 90 | 300 |
根据表中数据,我们得到的统计学的结论是:由__________的把握认为“使用微信支付与年龄有关”。
|
|
|
|
|
|
|
|
|
|
|
|
其中