题目内容
(2013•东至县一模)若直角坐标平面内M、N两点满足:
①点M、N都在函数f(x)的图象上;
②点M、N关于原点对称,则称这两点M、N是函数f(x)的一对“靓点”.
已知函数f(x)=
则函数f(x)有
①点M、N都在函数f(x)的图象上;
②点M、N关于原点对称,则称这两点M、N是函数f(x)的一对“靓点”.
已知函数f(x)=
|
一
一
对“靓点”.分析:根据“靓点”的定义可设y=x-3上任取一点M(x,y)(x>0),则关于原点对称的点为N(-x,-y),点N(-x,-y)在函数f(x)的图象上,转化成方程3-x=3-x(x>0)解的个数,然后转化成y=3-x,y=3-x(x>0)的图象的交点个数即可.
解答:解:设y=x-3上任取一点M(x,y)(x>0)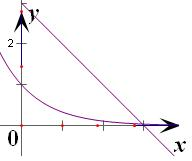
则关于原点对称的点为N(-x,-y),
根据“靓点”的定义可知点N(-x,-y)在函数f(x)的图象上,
则f(-x)=3-x=-y
∴
即3-x=3-x(x>0)
方程3-x=3-x(x>0)解的个数可看成y=3-x,y=3-x(x>0)的图象的交点个数
作出y=3-x,y=3-x(x>0)的图象可知有且只有一个交点
故函数f(x)有一对“靓点”.
故答案为:一

则关于原点对称的点为N(-x,-y),
根据“靓点”的定义可知点N(-x,-y)在函数f(x)的图象上,
则f(-x)=3-x=-y
∴
|
方程3-x=3-x(x>0)解的个数可看成y=3-x,y=3-x(x>0)的图象的交点个数
作出y=3-x,y=3-x(x>0)的图象可知有且只有一个交点
故函数f(x)有一对“靓点”.
故答案为:一
点评:本题主要考查了新定义,以及函数图象,同时考查了函数与方程的思想,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 (2013•东至县一模)若函数f(x)=a(x+1)p(x-1)q(a>0)在区间[-2,1]上的图象如图所示,则p,q的值可能是( )
(2013•东至县一模)若函数f(x)=a(x+1)p(x-1)q(a>0)在区间[-2,1]上的图象如图所示,则p,q的值可能是( )