题目内容
(本小题满分12分)
数列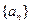 为等差数列,
为等差数列,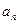 为正整数,其前
为正整数,其前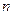 项和为
项和为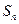 ,数列
,数列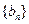 为等比数列,且
为等比数列,且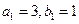 ,数列
,数列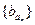 是公比为64的等比数列,
是公比为64的等比数列,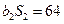 。
。
(1)求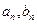 ;
;
(2)求证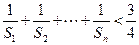 。
。
数列
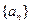 为等差数列,
为等差数列,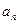 为正整数,其前
为正整数,其前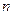 项和为
项和为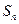 ,数列
,数列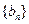 为等比数列,且
为等比数列,且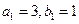 ,数列
,数列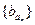 是公比为64的等比数列,
是公比为64的等比数列,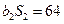 。
。(1)求
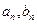 ;
;(2)求证
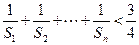 。
。(1)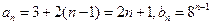
(2)证明见解析。
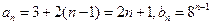
(2)证明见解析。
(1)设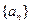 的公差为
的公差为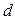 ,
,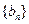 的公比为
的公比为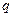 ,则
,则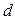 为正整数,
为正整数,
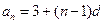 ,
,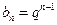
依题意有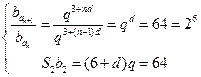 ①
①
由 知
知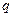 为正有理数,故
为正有理数,故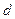 为
为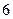 的因子
的因子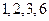 之一,
之一,
解①得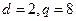
故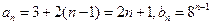
(2)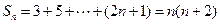
∴
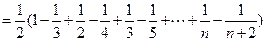
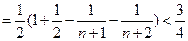
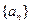 的公差为
的公差为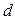 ,
,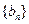 的公比为
的公比为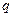 ,则
,则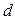 为正整数,
为正整数,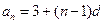 ,
,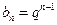
依题意有
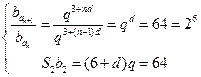 ①
①由
 知
知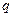 为正有理数,故
为正有理数,故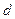 为
为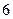 的因子
的因子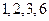 之一,
之一,解①得
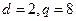
故
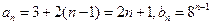
(2)
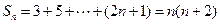
∴

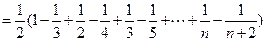
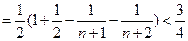

练习册系列答案
相关题目
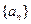 是调和数列,对于各项都是正数的数列
是调和数列,对于各项都是正数的数列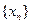 ,满足
,满足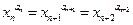
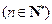 .
.
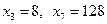 时,求第
时,求第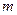 行各数的和;
行各数的和;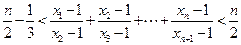 .
.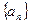 与
与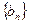 中,
中,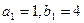 ,数列
,数列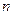 项和
项和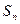 满足
满足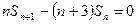 ,
,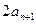 为
为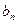 与
与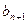 的等比中项,
的等比中项,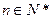 .
.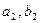 的值;
的值;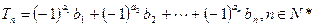 .证明
.证明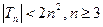 .
.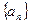 的各项均为正数,
的各项均为正数,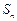 为其前
为其前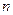 项和,对于任意
项和,对于任意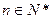 ,总有
,总有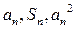 成等差数列.
成等差数列.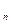 =a
=a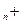 4
4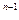 (
(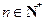 ), B
), B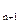 ≤4B
≤4B ,对任意
,对任意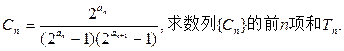
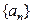 的前n项和为
的前n项和为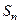 ;设
;设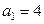 ,问
,问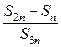 是否可能为一与n无关的常数?若不存在,说明理由.若存在,求出所有这样的数列的通项公式.
是否可能为一与n无关的常数?若不存在,说明理由.若存在,求出所有这样的数列的通项公式.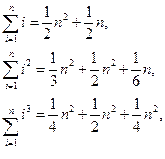
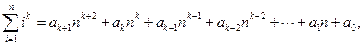
 ,ak-2= 。
,ak-2= 。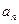 }的前n项和满足
}的前n项和满足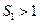 ,且
,且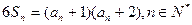
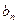 }满足
}满足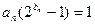 ,并记
,并记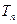 为{
为{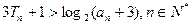 . (7分)
. (7分)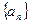 的前n项和为
的前n项和为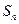 ,且
,且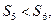
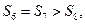 则下面说法错误的是( )
则下面说法错误的是( )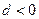
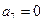

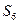 与
与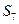 均为
均为