题目内容
(本小题满分10分)
已知圆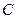 与直线
与直线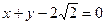 相切于点
相切于点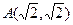 ,且圆心在直线
,且圆心在直线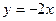 上.
上.
(Ⅰ)求圆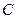 的方程;
的方程;
(Ⅱ)设直线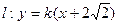 与圆
与圆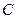 相交于
相交于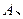
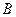 两点,
两点,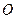 是坐标原点.求
是坐标原点.求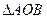 的面积最大值,并求取得最大值时直线
的面积最大值,并求取得最大值时直线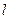 的方程.
的方程.
已知圆
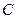 与直线
与直线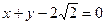 相切于点
相切于点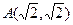 ,且圆心在直线
,且圆心在直线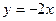 上.
上.(Ⅰ)求圆
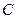 的方程;
的方程;(Ⅱ)设直线
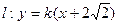 与圆
与圆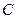 相交于
相交于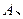
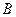 两点,
两点,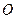 是坐标原点.求
是坐标原点.求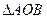 的面积最大值,并求取得最大值时直线
的面积最大值,并求取得最大值时直线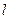 的方程.
的方程.(Ⅰ)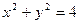
(Ⅱ)当且仅当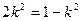 即
即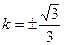 时,
时,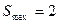 .
.
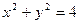
(Ⅱ)当且仅当
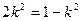 即
即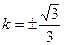 时,
时,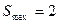 .
.解:(Ⅰ)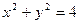 .
.
(Ⅱ)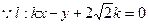 ,
,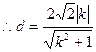 ,
,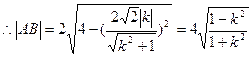 ,
,
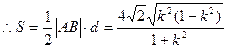 .
.
由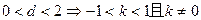 .
.
设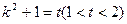 ,则
,则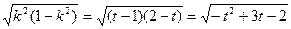 ,
,
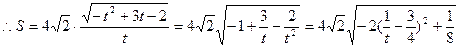 ,
,
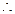 当
当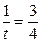 ,即
,即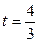 ,
,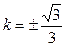 时,
时,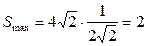 ,
,
∴S的最大值为2,取得最大值时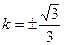 .所求直线
.所求直线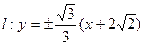 .
.
另解: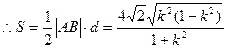
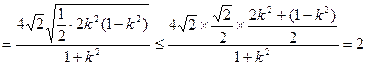 .
.
当且仅当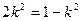 即
即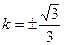 时,
时,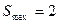 .
.
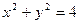 .
.(Ⅱ)
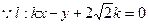 ,
,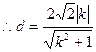 ,
,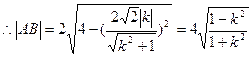 ,
,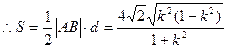 .
.由
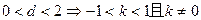 .
.设
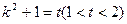 ,则
,则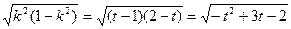 ,
,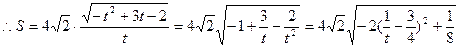 ,
,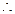 当
当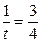 ,即
,即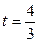 ,
,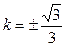 时,
时,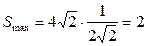 ,
,∴S的最大值为2,取得最大值时
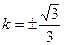 .所求直线
.所求直线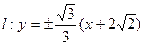 .
.另解:
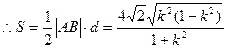
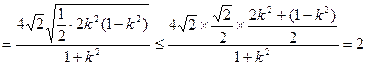 .
.当且仅当
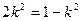 即
即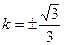 时,
时,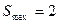 .
.
练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
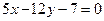 相切的圆的方程为_____________
相切的圆的方程为_____________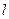 过点
过点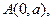 斜率为1,圆
斜率为1,圆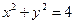 上恰有3个点到
上恰有3个点到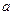 的值为( )
的值为( )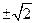
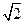
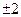
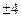
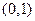 的直
的直 线与圆
线与圆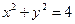 相交于
相交于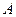 ,
,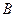 两点,则
两点,则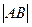 的最小值为 ( )
的最小值为 ( )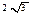
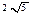
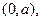 其斜率为1,且与圆
其斜率为1,且与圆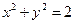 相切,则
相切,则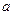 的值为
的值为 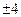

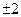
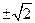
 1,2)的圆
1,2)的圆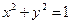 的切线方程为
的切线方程为  .
.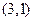 作一直线与圆
作一直线与圆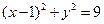 相交于M、N两点,则
相交于M、N两点,则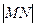 的最小值为( )
的最小值为( )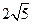
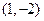 为圆心,且与直线
为圆心,且与直线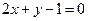 相切的圆的方程是 .
相切的圆的方程是 . 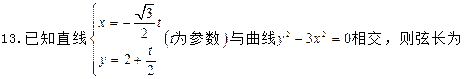 .
.