题目内容
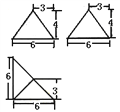
【题目】如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是![]() ,D是AC的中点。
,D是AC的中点。

(1)求证:B1C∥平面A1BD;
(2)求二面角A1-BD-A的大小;
(3)在线段AA1上是否存在一点E,使得平面B1C1E⊥平面A1BD,若存在,求出AE的长;若不存在,说明理由。
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)连结AB1交A1B于M,连结B1C,DM,由已知条件得四边形AA1B1B是矩形,由三角形中位线能证明B1C∥平面A1BD.(2)作CO⊥AB于O,建立空间直角坐标系O-xyz.利用向量法能求出二面角A1-BD-A的大小.(3)设E(1,x,0),求出平面B1C1E的法向量,利用向量法能求出存在点E,使得平面B1C1E⊥平面A1BD,且AE=![]()
试题解析:
(1)连结AB1交A1B于M,连结DM,
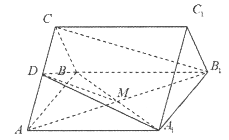
因为三棱柱ABC-A1B1C1是正三棱柱,
所以四边形AA1B1B是矩形,所以M为AB1的中点。
因为D是AC的中点,所以MD是三角形AB1C的中位线,
所以MD∥B1C。
因为MD![]() 平面A1BD,B1C
平面A1BD,B1C![]() 平面A1BD,所以B1C∥平面A1BD。
平面A1BD,所以B1C∥平面A1BD。
(2)作CO⊥AB于O,所以CO⊥平面ABB1A1,
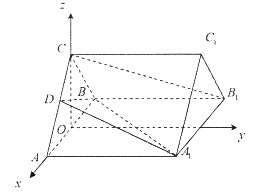
所以在正三棱柱ABC-A1B1C1中如图建立空间直角坐标系O-xyz。
因为AB=2,AA1=![]() ,D是AC的中点。
,D是AC的中点。
所以A(1,0,0),B(-l,0,0),C(0,0, ![]() ),A1(1,
),A1(1, ![]() ,0),
,0),
所以D(![]() ,0,
,0, ![]() ),
),![]() =(
=(![]() ,0,
,0, ![]() ),
),![]() =(2,
=(2, ![]() ,0)。
,0)。
设n=(x,y,z)是平面A1BD的法向量,
所以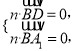 即
即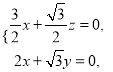 ,令x=-
,令x=-![]() ,则y=2,z=3,
,则y=2,z=3,
所以n=(-![]() ,2,3)是平面A1BD的一个法向量。
,2,3)是平面A1BD的一个法向量。
由题意可知![]() =(0,
=(0, ![]() ,0)是平面ABD的一个法向量,
,0)是平面ABD的一个法向量,
所以cos<n, ![]() >=
>=![]() =
=![]() 。
。
由题知二面角A1-BD-A为锐角,所以它的大小为![]() 。
。
(3)设E(1,x,0),则![]() =(1,x-
=(1,x-![]() ,-
,-![]() ),
),![]() =(-1,0,-
=(-1,0,-![]() ),
),
设平面B1C1E的法向量m=(x1,y1,z1),
所以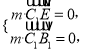 即
即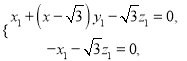 令z1=-
令z1=-![]() ,则x1=3,y1=
,则x1=3,y1=![]() ,
,
m=(3, ![]() ,-
,-![]() ),又m·n=0,即-3
),又m·n=0,即-3![]() +
+![]() -3
-3![]() =0,解得x=
=0,解得x=![]() ,
,
所以存在点E,使得平面B1C1E⊥平面A1BD且AE=![]() 。
。