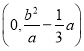题目内容
【题目】一个正四面体的四个面上分别标有1，2，3，4，将该正四面体抛掷两次，则向下一面的数字和为偶数的概率为_________，这两个数字和的数学期望为__________.
【答案】
5
【解析】
写出基本事件，然后计算出事件“正四面体抛掷两次，则向下一面的数字和为偶数”的基本事件，利用古典概型计算公式求出概率；先求出两个数字和的可以有取值，并求出概率，利用数学期望的计算公式求出这两个数字和的数学期望值.
该正四面体抛掷两次，出现的可能情况如下：
共16种情况，向下一面的数字和为偶数的有
共8种情况，故该正四面体抛掷两次，则向下一面的数字和为偶数的概率为
.设该正四面体抛掷两次，则向下一面的数字和为
,它的可能到值为2，3，4，5，6，7，8
，
，
.
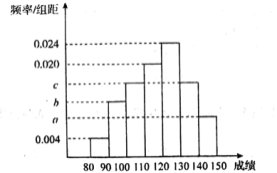
【题目】高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示，成绩分组区间为：
.其中a，b，c成等差数列且
.物理成绩统计如表.（说明：数学满分150分，物理满分100分）
分组 |
|
|
|
|
|
频数 | 6 | 9 | 20 | 10 | 5 |
（1）根据频率分布直方图，请估计数学成绩的平均分；
（2）根据物理成绩统计表，请估计物理成绩的中位数；
（3）若数学成绩不低于140分的为“优”，物理成绩不低于90分的为“优”，已知本班中至少有一个“优”同学总数为6人，从此6人中随机抽取3人，记X为抽到两个“优”的学生人数，求X的分布列和期望值.
【题目】为了增强消防意识，某部门从男职工中随机抽取了50人，从女职工中随机抽取了40人参加消防知识测试，按优秀程度制作了如下
列联表：
优秀 | 非优秀 | 总计 | |
男职工 | 35 | ||
女职工 | |||
总计 | 50 |
（1）完成列联表；
（2）判断是否有
的把握认为消防知识是否优秀与性别有关.
附：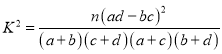
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
