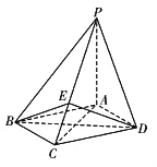
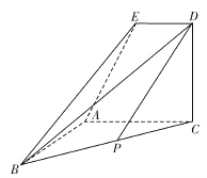
题目内容
【题目】已知椭圆C:![]() (
(![]() )的左、右顶点分别为A,B,左焦点为F,O为原点,点P为椭圆C上不同于A、B的任一点,若直线PA与PB的斜率之积为
)的左、右顶点分别为A,B,左焦点为F,O为原点,点P为椭圆C上不同于A、B的任一点,若直线PA与PB的斜率之积为![]() ,且椭圆C经过点
,且椭圆C经过点![]() .
.
(1)求椭圆C的方程;
(2)若P点不在坐标轴上,直线PA,PB交y轴于M,N两点,若直线OT与过点M,N的圆G相切.切点为T,问切线长![]() 是否为定值,若是,求出定值,若不是,请说明理由.
是否为定值,若是,求出定值,若不是,请说明理由.
【答案】(1)![]() ;(2)是定值,定值为3
;(2)是定值,定值为3
【解析】
(1)由斜率之积可求得![]() ,
,![]() 的关系,将
的关系,将![]() 代入可再得
代入可再得![]() ,
,![]() 的关系,解出
的关系,解出![]() ,
,![]() 的值,即可求出椭圆的方程;
的值,即可求出椭圆的方程;
(2)由(1)得![]() ,
,![]() 的坐标,设
的坐标,设![]() ,满足椭圆的方程,得直线
,满足椭圆的方程,得直线![]() ,
,![]() ,求出
,求出![]() ,
,![]() 的坐标,再用圆中切割线定理得切线长的值.
的坐标,再用圆中切割线定理得切线长的值.
(1)设![]() ,由题意得
,由题意得![]() ,
,![]() ,
,![]() ,
,
![]()
![]() 而
而![]() 得:
得:![]() ①,
①,
又过![]() ②,所以由①②得:
②,所以由①②得:![]() ,
,![]() ;
;
所以椭圆![]() 的方程:
的方程:![]() ;
;
(2)由(1)得:![]() ,
,![]() 设
设![]() ,
,![]() ,则直线的方程
,则直线的方程![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]() 的坐标
的坐标![]() ,
,
直线![]() 的方程:
的方程:![]() ,令
,令![]() ,
,![]() ,所以坐标
,所以坐标![]() ,
,
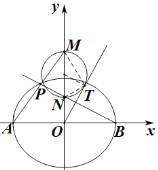
![]() (圆的切割线定理),再联立
(圆的切割线定理),再联立![]() ,
,
![]()

【题目】同程旅游随机调查了年龄在![]() (单位:岁)内的1250人的购票情况,其中50岁以下(不包含50岁)的有900人,50岁以上(包含50岁)的有350人,由调查数据的统计结果显示,有
(单位:岁)内的1250人的购票情况,其中50岁以下(不包含50岁)的有900人,50岁以上(包含50岁)的有350人,由调查数据的统计结果显示,有![]() 的人参与网上购票,网上购票人数的频率分布直方图如下图所示.
的人参与网上购票,网上购票人数的频率分布直方图如下图所示.

(1)已知年龄在![]() ,
,![]() ,
,![]() 的网上购票人数成等差数列,求
的网上购票人数成等差数列,求![]() 的值;
的值;
(2)根据题目数据填写![]() 列联表,并根据填写数据判断能否在犯错误的概率不超过0.001的前提下,认为网上购票与年龄有关系?
列联表,并根据填写数据判断能否在犯错误的概率不超过0.001的前提下,认为网上购票与年龄有关系?
50岁以下 | 50岁以上 | 总计 | |
参与网上购票 | |||
不参与网上购票 | |||
总计 |
附: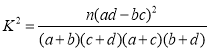
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
(3)为鼓励大家网上购票,该平台常采用购票就发放酒店入住代金券的方法进行促销,具体做法如下:年龄在![]() 岁的每人发放20元,其余年龄段的每人发放50元,先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取10人,并在这10人中随机抽取3人进行回访调查,求此3人获得代金券的金额总和
岁的每人发放20元,其余年龄段的每人发放50元,先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取10人,并在这10人中随机抽取3人进行回访调查,求此3人获得代金券的金额总和![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
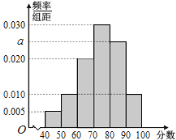
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |