题目内容
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 是
是![]() 上的一点.
上的一点.
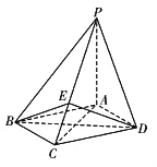
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 平面
平面![]() ,且
,且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)利用面面垂直的性质定理得出![]() 平面
平面![]() ,再由面面垂直的判定定理证明平面
,再由面面垂直的判定定理证明平面![]() 平面
平面![]() ;
;
(2)设![]() 与
与![]() 交于
交于![]() 点,连接
点,连接![]() ,由线面平行的性质以及中位线定理得出点
,由线面平行的性质以及中位线定理得出点![]() 为
为![]() 中点,再由勾股定理以及面面垂直的性质得出
中点,再由勾股定理以及面面垂直的性质得出![]() 底面
底面![]() ,进而得出
,进而得出![]() 为直线
为直线![]() 与平面
与平面![]() 所成角,再由直角三角的边角关系得出直线
所成角,再由直角三角的边角关系得出直线![]() 与平面
与平面![]() 所成角.
所成角.
(1)因为底面![]() 为菱形,所以
为菱形,所以![]()
又平面![]() 底面
底面![]() ,
,![]() 底面
底面![]()
所以![]() 平面
平面![]()
又![]() 平面
平面![]()
所以平面![]() 平面
平面![]() .
.
(2)设![]() 与
与![]() 交于
交于![]() 点,连接
点,连接![]()
直线![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
所以![]() ,即点
,即点![]() 为
为![]() 中点,
中点,![]()
因![]() ,
,![]() ,则
,则![]() 为等腰直角三角形,则
为等腰直角三角形,则![]() ,
,
因为平面![]() 底面
底面![]() ,则
,则![]() 底面
底面![]()
又因为![]() ,则
,则![]() 底面
底面![]()
则![]() 为直线
为直线![]() 与平面
与平面![]() 所成角.
所成角.
底面![]() 为菱形,
为菱形,![]() ,则
,则![]() .
.
所以![]() ,故
,故![]() .
.
则直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】中国武汉于2019年10月18日至2019年10月27日成功举办了第七届世界军人运动会.来自109个国家的9300余名运动员同台竞技.经过激烈的角逐,奖牌榜的前3名如下:
国家 | 金牌 | 银牌 | 铜牌 | 奖牌总数 |
中国 | 133 | 64 | 42 | 239 |
俄罗斯 | 51 | 53 | 57 | 161 |
巴西 | 21 | 31 | 36 | 88 |
某数学爱好者采用分层抽样的方式,从中国和巴西获得金牌选手中抽取了22名获奖代表.从这22名中随机抽取3人, 则这3人中中国选手恰好1人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整,调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额,依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
… | … | … | … | … | … |
某税务部门在某公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
(1)若某员工2月的工资、薪金等税前收入为7500元时,请计算一下调整后该员工的实际收入比调整前增加了多少?
(2)现从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用
的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,
元的人数,![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,设随机变量
元的人数,设随机变量![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
【题目】世界互联网大会是由中国倡导并每年在浙江省嘉兴市桐乡乌镇举办的世界性互联网盛会,大会旨在搭建中国与世界互联互通的国际平台和国际互联网共享共治的中国平台,让各国在争议中求共识在共识中谋合作在合作中创共赢.2019年10月20日至22日,第六届世界互联网大会如期举行,为了大会顺利召开,组委会特招募了1 000名志愿者.某部门为了了解志愿者的基本情况,调查了其中100名志愿者的年龄,得到了他们年龄的中位数为34岁,年龄在![]() 岁内的人数为15,并根据调查结果画出如图所示的频率分布直方图:
岁内的人数为15,并根据调查结果画出如图所示的频率分布直方图:

(1)求![]() ,
,![]() 的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
(2)这次大会志愿者主要通过现场报名和登录大会官网报名,即现场和网络两种方式报名调查.这100位志愿者的报名方式部分数据如下表所示,完善下面的表格,通过计算说明能
否在犯错误的概率不超过0.001的前提下,认为“选择哪种报名方式与性别有关系”?
男性 | 女性 | 总计 | |
现场报名 | 50 | ||
网络报名 | 31 | ||
总计 | 50 |
参考公式及数据: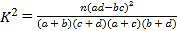 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
【题目】某保险公司有一款保险产品的历史收益率(收益率![]() 利润
利润![]() 保费收入)的频率分布直方图如图所示:
保费收入)的频率分布直方图如图所示:
(1)试估计这款保险产品的收益率的平均值;
(2)设每份保单的保费在20元的基础上每增加![]() 元,对应的销量为
元,对应的销量为![]() (万份).从历史销售记录中抽样得到如下5组
(万份).从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表,知![]() 与
与![]() 有较强的线性相关关系,且据此计算出的回归方程为
有较强的线性相关关系,且据此计算出的回归方程为![]() .
.

(ⅰ)求参数![]() 的值;
的值;
(ⅱ)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入
的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入![]() 每份保单的保费
每份保单的保费![]() 销量.
销量.