题目内容
已知直线
：
和圆C: 
，则直线和圆C的位置关系为（ ）.
| A．相交 | B．相切 | C．相离 | D．不能确定 |
A
解析试题分析：根据题意，由于直线：和圆C: ，圆心为原点，半径为1，那么圆心到直线的距离为d=
<1，故可知直线与圆相交，故答案为A.
考点：直线与圆位置关系
点评：主要是考查了直线与圆的位置关系的运用，属于基础题。
练习册系列答案
相关题目
与圆
交于不同的两点
若
,
是坐标原点,那么实数
的取值范围是（ ）
直线
与圆
的位置关系是（ ）
| A．相离 | B．相交 | C．相切 | D．不确定 |
直线
与圆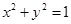
交于不同两点
、
，
为坐标原点，则“
”是“向量
、
满足
”的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
直线：3x-4y-9=0与圆：
(
为参数)的位置关系是（ ）
| A．相切 | B．相离 | C．相交 | D．相交且过圆心 |
，在上任取一点
，线段
长度的最小值称为点
．设是长为2的线段，点集
所表示图形的面积为（ ）
能够使圆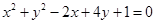
上恰有两点到直线
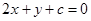距离等于1的
的一个值为 ( )
A． | B． | C． | D． |
当曲线y=
与直线kx-y-2k+3=0有两个相异的交点时，实数k的取值范围是 ( )
A．(0, ) | B．( , ] | C．(,] | D．(,+∞) |
已知圆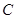
与直线
都相切，圆心在直线
上，则圆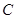的方程为（ ）
A． | B． |
C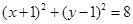． | D． |