题目内容
已知函数y=f(x)满足方程f(x)+(x-3)f(1)=x3+x-4(x∈R).(I)求f(x)的解析式;
(II)若函数y=f(x)在区间[-1,m]上的值域为[2-
2
| ||
| 9 |
2
| ||
| 9 |
(III)记g(x)=f(x)-bx2+(2c+1)x-2,若g'(x)的两个零点x1,x2满足x1≠x2,且x1,x2∈[-1,2],求b+2c的取值范围.
分析:(I)令x=1,求出f(1)的值,然后代入,即可求出函数的解析式;
(II)先利用导数研究函数的单调性,然后结合图形可知由f(x)=2+
,解得x的值即可求出m的范围;
(III)根据g′(x)=0在[-1,2]上有两个不等的实根,建立a、b的约束关系,画出区域,根据线性规划的知识可求出b+2c的取值范围.
(II)先利用导数研究函数的单调性,然后结合图形可知由f(x)=2+
2
| ||
| 9 |
(III)根据g′(x)=0在[-1,2]上有两个不等的实根,建立a、b的约束关系,画出区域,根据线性规划的知识可求出b+2c的取值范围.
解答:解:(I)令x=1得f(1)-2f(1)=-2
解得f(1)=2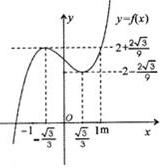
∴f(x)=x3-x+2
(II)f′(x)=3x2-1,由f′(x)>0
解得x>
或x<-
由f′(x)>0
解得-
<x<
∴f(x)在(-∞,-
),(
,+∞)上是增函数,
在(-
,
)上是减函数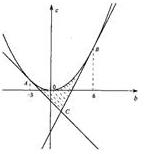
f(x)极大值为f(-
)=2+
f(x)极小值为f(
)=2-
由f(x)=2+
,解得x=-
或x=
∴m的取值范围是[-
,
]
(III)g(x)=f(x)-bx2+(2c+1)x-2=x3-bx2+2cx
g′(x)=3x2-2bx+2c
依题意g′(x)=0在[-1,2]上有两个不等的实根
∴
画出(b、c)的可行域
b+2c∈[-
,18)
解得f(1)=2

∴f(x)=x3-x+2
(II)f′(x)=3x2-1,由f′(x)>0
解得x>
| ||
| 3 |
| ||
| 3 |
由f′(x)>0
解得-
| ||
| 3 |
| ||
| 3 |
∴f(x)在(-∞,-
| ||
| 3 |
| ||
| 3 |
在(-
| ||
| 3 |
| ||
| 3 |

f(x)极大值为f(-
| ||
| 3 |
2
| ||
| 9 |
f(x)极小值为f(
| ||
| 3 |
2
| ||
| 9 |
由f(x)=2+
2
| ||
| 9 |
| ||
| 3 |
2
| ||
| 3 |
∴m的取值范围是[-
| ||
| 3 |
2
| ||
| 3 |
(III)g(x)=f(x)-bx2+(2c+1)x-2=x3-bx2+2cx
g′(x)=3x2-2bx+2c
依题意g′(x)=0在[-1,2]上有两个不等的实根
∴
|
画出(b、c)的可行域
b+2c∈[-
| 9 |
| 2 |
点评:本题主要考查了函数的解析式以及利用导数研究函数的单调性和极值,同时考查了利用线性规划求取值范围,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足