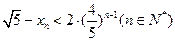题目内容
(本小题满分12分)
已知数列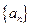 中,
中,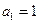 ,
,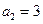 ,其前
,其前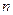 项和为
项和为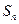 ,且当
,且当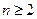 时,
时,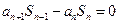 .
.
(Ⅰ)求证:数列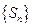 是等比数列;
是等比数列;
(Ⅱ)求数列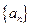 的通项公式;
的通项公式;
(Ⅲ)令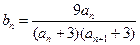 ,记数列
,记数列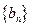 的前
的前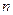 项和为
项和为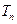 ,证明对于任意的正整数
,证明对于任意的正整数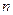 ,都有
,都有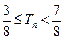 成立.
成立.
已知数列
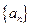 中,
中,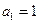 ,
,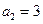 ,其前
,其前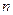 项和为
项和为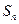 ,且当
,且当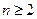 时,
时,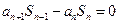 .
.(Ⅰ)求证:数列
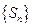 是等比数列;
是等比数列;(Ⅱ)求数列
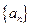 的通项公式;
的通项公式;(Ⅲ)令
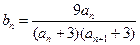 ,记数列
,记数列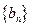 的前
的前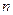 项和为
项和为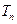 ,证明对于任意的正整数
,证明对于任意的正整数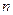 ,都有
,都有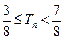 成立.
成立..(Ⅰ)证明:当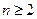 时,
时,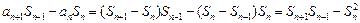 ,
,
所以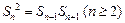 .
.
又由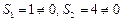 ,可推知对一切正整数
,可推知对一切正整数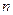 均有
均有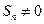 ,
,
∴数列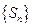 是等比数列. ………3分
是等比数列. ………3分
(Ⅱ)解:由(Ⅰ)知等比数列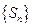 的首项为1,公比为4,
的首项为1,公比为4,
∴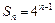 .
.
当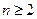 时,
时,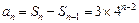 ,
,
又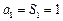 ,
,
∴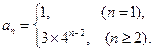 ………6分
………6分
(Ⅲ)证明:当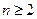 时,
时,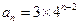 ,此时
,此时
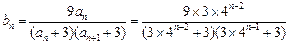
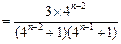 ,
,
又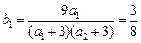 ,
,
∴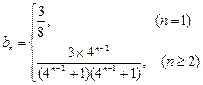 . ………8分
. ………8分
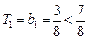 ,
,
当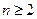 时,
时,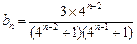 =
=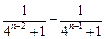
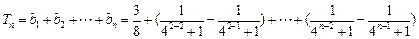
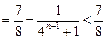 . ……… 11分
. ……… 11分
又因为对任意的正整数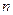 都有
都有 所以
所以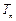 单调递增,即
单调递增,即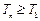 ,
,
所以对于任意的正整数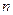 ,都有
,都有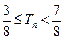 成立. ……… 12分
成立. ……… 12分
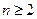 时,
时,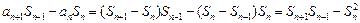 ,
,所以
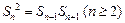 .
.又由
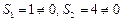 ,可推知对一切正整数
,可推知对一切正整数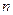 均有
均有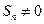 ,
,∴数列
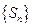 是等比数列. ………3分
是等比数列. ………3分(Ⅱ)解:由(Ⅰ)知等比数列
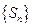 的首项为1,公比为4,
的首项为1,公比为4, ∴
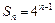 .
.当
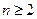 时,
时,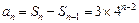 ,
,又
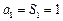 ,
,∴
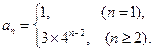 ………6分
………6分(Ⅲ)证明:当
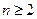 时,
时,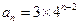 ,此时
,此时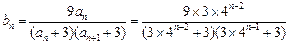
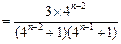 ,
,又
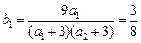 ,
,∴
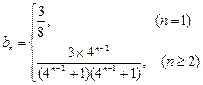 . ………8分
. ………8分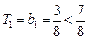 ,
,当
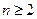 时,
时,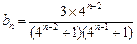 =
=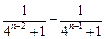
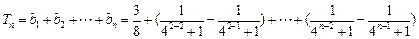
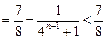 . ……… 11分
. ……… 11分又因为对任意的正整数
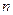 都有
都有 所以
所以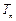 单调递增,即
单调递增,即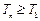 ,
,所以对于任意的正整数
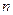 ,都有
,都有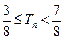 成立. ……… 12分
成立. ……… 12分略

练习册系列答案
相关题目
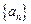 满足
满足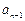 +
+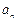 =4n-3(n∈
=4n-3(n∈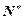 ).
).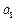 的值;
的值;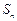 ;
;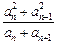 ≥5成立,求
≥5成立,求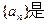 等比数列,其中
等比数列,其中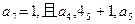 成等差数列.
成等差数列.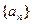 的通项公式;
的通项公式;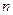 项和记为
项和记为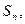 证明:
证明: 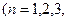 …).
…).
 的首项
的首项 为
为 (
( ),且
),且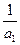 ,
, ,
, 成等比数列(Ⅰ)求数列
成等比数列(Ⅰ)求数列 ,试比较
,试比较 与
与 )个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
 ,求和
,求和 (
( );(其中
);(其中 表示所有的积
表示所有的积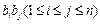 的和)
的和)
 的前n项和为
的前n项和为 ,则
,则 等于( )
等于( ) ,首项为19,公差是整数,从第6项开始为负值,则公差为( ).
,首项为19,公差是整数,从第6项开始为负值,则公差为( ).



 ,
, 为实数,首项为
为实数,首项为 的前
的前 项和为
项和为 ,满足
,满足 .
. , 求
, 求 及
及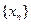 满足:
满足: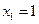 ,
, .
.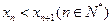 ;
;