题目内容
已知直线l1:2x-3y-6=0和直线l2:y+1=0则抛物线y=| 1 | 4 |
分析:先确定y=-1为抛物线的准线,再由抛物线的定义得到P到l2的距离等于P到抛物线的焦点F(0,1)的距离,进而转化为在抛物线上找一个点P使得P到点F(0,1)和直线l2的距离之和最小,再由点到线的距离公式可得到距离的最小值.
解答:解:直线l2:y+1=0为抛物线抛物线y=
x2的准线,
由抛物线的定义知,P到l2的距离等于P到抛物线的焦点F(0,1)的距离,
故本题化为在抛物线y=
x2上找一个点P使得P到点F(0,1)和直线l2的距离之和最小,
最小值为F(0,1)到直线l2:2x-3y-6=0的距离,
即d=
=
,
故答案为:
.
| 1 |
| 4 |
由抛物线的定义知,P到l2的距离等于P到抛物线的焦点F(0,1)的距离,
故本题化为在抛物线y=
| 1 |
| 4 |
最小值为F(0,1)到直线l2:2x-3y-6=0的距离,
即d=
| |0-3-6| | ||
|
9
| ||
| 13 |
故答案为:
9
| ||
| 13 |
点评:本小题考查抛物线的定义、点到直线的距离,考查基础知识的综合应用.圆锥曲线是高考的热点也是难点问题,一定要强化复习.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知直线l1:2x-my+1=0与l2:x+(m-1)y-1=0,则“m=2”是“l1⊥l2”的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充分且必要条件 | D、既不充分又不必要条件 |
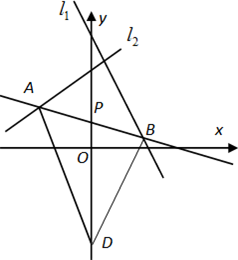 如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.
如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.