题目内容
(本小题满分13分)已知椭圆的中心在原点,焦点在y轴上,离心率为 ,且
,且
椭圆经过圆 的圆心C。
的圆心C。
(I)求椭圆的标准方程;
(II)设直线 与椭圆交于A、B两点,点
与椭圆交于A、B两点,点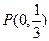 且|PA|=|PB|,求直线
且|PA|=|PB|,求直线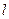 的方程。
的方程。
 ,且
,且椭圆经过圆
 的圆心C。
的圆心C。(I)求椭圆的标准方程;
(II)设直线
 与椭圆交于A、B两点,点
与椭圆交于A、B两点,点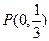 且|PA|=|PB|,求直线
且|PA|=|PB|,求直线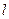 的方程。
的方程。(1)由圆C的方程可知:圆心C(1,-2) ————2分
设椭圆的方程为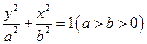
椭圆过圆心C,可得: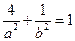
另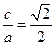 ,且
,且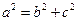 。
。
解得: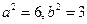
即椭圆的方程为: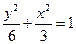 ————6分
————6分
(2)将直线方程与椭圆方程联立方程组消元可得:
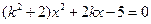
设
法一:设AB中点M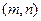
其中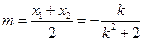 ,
,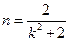 ————8分
————8分
若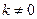 ,则有:
,则有: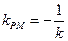 ,解得:
,解得: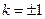 ————10分
————10分
若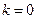 ,显然满足题意。
,显然满足题意。
故直线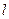 的方程为:
的方程为: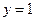 或
或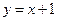 或
或 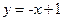 ————13分
————13分
法二:由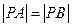 ,代入可得方程:可解出
,代入可得方程:可解出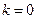 或
或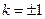
设椭圆的方程为
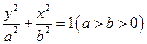
椭圆过圆心C,可得:
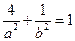
另
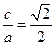 ,且
,且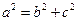 。
。解得:
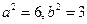
即椭圆的方程为:
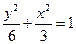 ————6分
————6分(2)将直线方程与椭圆方程联立方程组消元可得:
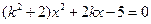
设
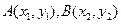
法一:设AB中点M
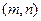
其中
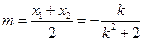 ,
,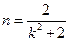 ————8分
————8分若
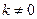 ,则有:
,则有: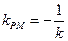 ,解得:
,解得: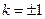 ————10分
————10分若
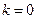 ,显然满足题意。
,显然满足题意。故直线
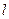 的方程为:
的方程为: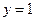 或
或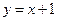 或
或 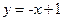 ————13分
————13分法二:由
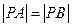 ,代入可得方程:可解出
,代入可得方程:可解出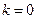 或
或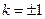
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
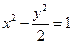 ,过
,过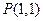 能否作一条直线
能否作一条直线 ,与双曲线交于
,与双曲线交于 两点,且点
两点,且点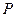 是线段
是线段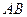 中点?若能,求出
中点?若能,求出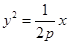 的焦点与椭圆
的焦点与椭圆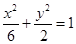 的右焦点重合,则p的值为( )
的右焦点重合,则p的值为( ) 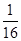 B
B 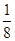 C
C 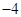 D 4
D 4

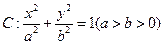 的离心率
的离心率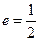 ,且椭圆过点
,且椭圆过点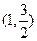 .
. 的方程;
的方程; 为椭圆
为椭圆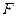 为椭圆的右焦点,以
为椭圆的右焦点,以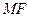 长为半径作圆
长为半径作圆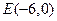 作圆
作圆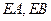 ,(
,(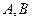 为切点),求点
为切点),求点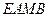 的面积最大.]
的面积最大.]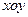 中,设点
中,设点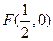 ,直线
,直线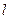 :
: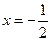 ,点
,点 在直线
在直线 是线段
是线段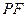 与
与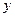 轴的交点,
轴的交点, 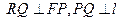 .
.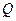 的轨迹的方程
的轨迹的方程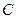 ;
;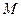 过
过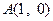 ,且圆心
,且圆心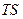 是圆
是圆 是否为定值?请说明理由.
是否为定值?请说明理由.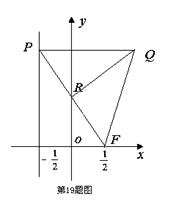
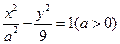 的离心率为2,则
的离心率为2,则 等于__________
等于__________ 的离心率为
的离心率为 则
则 的最小值为
的最小值为