题目内容
已知数列{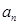 }的前n项和为Sn,若a1 =" -2" ,a2=2, 且an + 2-an=1+(-1)n 则S50 =
}的前n项和为Sn,若a1 =" -2" ,a2=2, 且an + 2-an=1+(-1)n 则S50 =
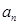 }的前n项和为Sn,若a1 =" -2" ,a2=2, 且an + 2-an=1+(-1)n 则S50 =
}的前n项和为Sn,若a1 =" -2" ,a2=2, 且an + 2-an=1+(-1)n 则S50 = 600
分析:通过对n的讨论是奇数函数偶数,判断出数列的奇数项是常数列,偶数项是等差数列,利用分组的方法将数列{an}分成两个数列,再利用等差数列的前n项和公式求出和.
解答:解:∵an+2-an=1+(-1)n
∴当n为偶数时,an+2-an=2;当n为奇数时,an+2-an=0
∴a1,a3,a5…为常数列-2;a2,a4,a6…为以2为首项,以2为公差的等差数列
∴S50=((a1+a3+a5…+a49)+(a2+a4+a6+…+a50)
=25×(-2)+2×25+
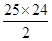 ×2
×2=600
故答案为600.
点评:求数列的前n项和,首项根据数列的通项特点.选择合适的求和方法,故关键是求出数列的通项.

练习册系列答案
相关题目
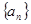 的前
的前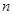 项和为
项和为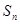 ,
,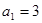 ,若数列
,若数列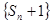 是公比为
是公比为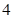 的等比数列.
的等比数列. 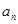 ;
;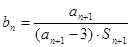 ,
,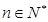 ,求数列
,求数列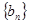 的前
的前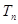 .
.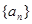 是的前n项和为Sn,满足
是的前n项和为Sn,满足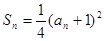
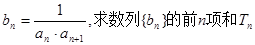
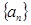 中,
中,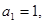 且点
且点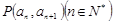 在直线
在直线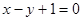 上。
上。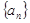 的通项公式;
的通项公式; (Ⅱ)若函数
(Ⅱ)若函数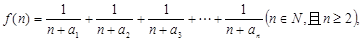 求函数
求函数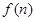 的最小值;
的最小值; (Ⅲ)设
(Ⅲ)设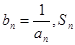 表示数列
表示数列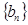 的前
的前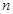 项和。试问:是否存在关于
项和。试问:是否存在关于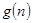 ,使得
,使得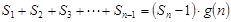 对于一切不小于2的自然数
对于一切不小于2的自然数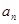 }的前n项和为
}的前n项和为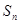 ,若
,若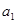 =" -11" ,
=" -11" ,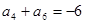 ,则当
,则当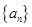 的首项及公差均是正整数,前
的首项及公差均是正整数,前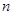 项和为
项和为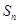 ,且
,且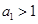 ,
,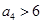 ,
,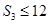 ,则
,则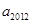 = .
= .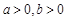 ,
,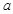 、
、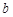 的等差中项等于
的等差中项等于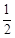 ,设
,设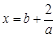 ,
,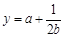 ,则
,则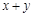 的最小值等于( )
的最小值等于( )



 是等比数列,且
是等比数列,且 则
则
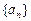 中,
中, 前5项和
前5项和 则其公差
则其公差