题目内容
【题目】已知
是定义在
上的偶函数，当
时，
.
（1）用分段函数形式写出的解析式；
（2）写出的单调区间；
（3）求出函数的最值.
【答案】（1）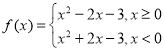
；（2）
的增区间为
，
，减区间为
，
；（3）最小值为-4，无最大值.
【解析】
（1）根据
是定义在
上的偶函数，且当
时，
，
设
，则
，通过
求解.
（2）每一段都是二次函数，根据二次函数的图象和性质求解.
（3）利用（2）的单调性求解.
（1）
是定义在上的偶函数，
当时，，
当时，设，则，
即时，
.
故.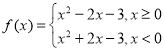
（2）如图所示：
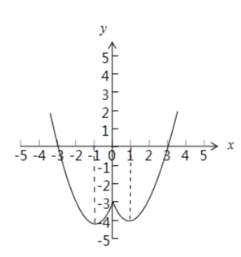
当时，，对称轴为
，
增区间为，减区间为；
当时，，对称轴为
，
增区间为，减区间为.
综上，的增区间为，，减区间为，.
（3）由（2）知，当时，，
，无最大值；
当时，，
，无最大值.
综上，函数的最小值为-4，无最大值.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
