题目内容
设S n是公差为d(d≠0)的无穷等差数列{a n}的前n项和,则下列命题错误的是
| A.若d<0,则数列{S n}有最大项 |
| B.若数列{S n}有最大项,则d<0 |
C.若数列{S n}是递增数列,则对任意的n N*,均有S n>0 N*,均有S n>0 |
D.若对任意的n N*,均有S n>0,则数列{S n}是递增数列 N*,均有S n>0,则数列{S n}是递增数列 |
C
解析试题分析:A项中d<0,数列是递减数列,若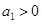 则存在
则存在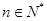 满足
满足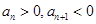
则 最大,若
最大,若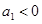 则
则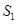 最大;B项中若
最大;B项中若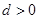 则
则 逐渐增大,无最大值;C项中当
逐渐增大,无最大值;C项中当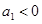 时
时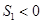 ,所以错误;D项中若数列是递减数列,则存在
,所以错误;D项中若数列是递减数列,则存在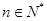 满足当
满足当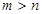 时
时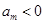 恒成立,存在
恒成立,存在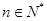 满足
满足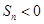
考点:数列单调性与求和
点评:当数列是递增数列时 存在最小值,当数列是递减数列时
存在最小值,当数列是递减数列时 存在最大值
存在最大值

练习册系列答案
相关题目
若数列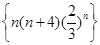 中的最大项是第
中的最大项是第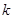 项,则
项,则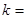 ( )
( )
| A.4 | B.5 | C.6 | D.7 |
已知数列 的通项公式为
的通项公式为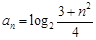 ,那么
,那么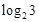 是这个数列的( )
是这个数列的( )
| A.第3项 | B.第4项 | C.第5项 | D.第6项 |
已知函数 的图象在点
的图象在点 处的切线的斜率为3,数列
处的切线的斜率为3,数列
的前 项和为
项和为 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知数列 满足
满足 ,
, ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知数列 的前
的前 项和为
项和为 ,且
,且 ,
,
 ,可归纳猜想出
,可归纳猜想出 的表达式为
的表达式为
A. | B. | C. | D. |
用火柴棒摆“金鱼”,如图所示:
按照上面的规律,第 个“金鱼”图需要火柴棒的根数为
个“金鱼”图需要火柴棒的根数为
A. | B.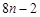 | C. | D. |




 }的前
}的前 项和
项和 ,则
,则 的值为 ;
的值为 ;