题目内容
已知函数 的图象在点
的图象在点 处的切线的斜率为3,数列
处的切线的斜率为3,数列
的前 项和为
项和为 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
B
解析试题分析:因为函数f(x)=x2+bx的图象在点A(1,f(1))处切线的斜率为3,
所以有f'(1)=2×1+b=3⇒b=1.
∴f(n)=n2+n,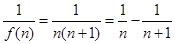
∴s2013=1-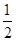 +
+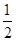 -
-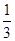 +……+
+……+ 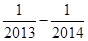 =
=
故选B.
考点:导数的几何意义,直线方程,裂项相消法。
点评:小综合题,本题综合性较强,综合考查导数的几何意义,直线方程,裂项相消法,难度不大,思路清晰,注意正确求得切线方程是关键。

练习册系列答案
相关题目
已知数列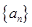 的前
的前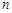 项和为
项和为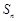 ,且
,且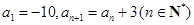 ,则
,则 取最小值时,
取最小值时,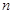 的值是( )
的值是( )
| A.3 | B.4 | C. 5 | D.6 |
设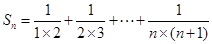
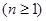 ,若
,若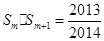 ,则
,则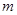 =( )
=( )
| A.2013 | B.2014 | C.4028 | D.4026 |
数列{an}的通项公式 (
( ),若前n项的和
),若前n项的和 ,则项数n为
,则项数n为
A.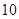 | B.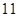 | C.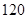 | D.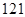 |
设S n是公差为d(d≠0)的无穷等差数列{a n}的前n项和,则下列命题错误的是
| A.若d<0,则数列{S n}有最大项 |
| B.若数列{S n}有最大项,则d<0 |
C.若数列{S n}是递增数列,则对任意的n N*,均有S n>0 N*,均有S n>0 |
D.若对任意的n N*,均有S n>0,则数列{S n}是递增数列 N*,均有S n>0,则数列{S n}是递增数列 |
将石子摆成如图的梯形形状,称数列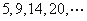 为“梯形数”.根据图形的构成,数列的第10项为( )
为“梯形数”.根据图形的构成,数列的第10项为( )


A.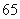 | B.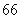 | C.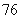 | D. |
若数列 中,
中, ,则
,则 取得最大值时
取得最大值时 的值是( )
的值是( )
| A. 13 | B. 14 | C. 15 | D. 14或15 |
已知数列{an}的通项公式是an=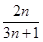 ,那么这个数列是( )
,那么这个数列是( )
| A.递增数列 | B.递减数列 |
| C.摆动数列 | D.常数列 |
 依它的前10项的规律,这个数列的第2014项
依它的前10项的规律,这个数列的第2014项 ="__________."
="__________."  _________.
_________.