题目内容
已知数列 的前
的前 项和为
项和为 ,且
,且 ,
,
 ,可归纳猜想出
,可归纳猜想出 的表达式为
的表达式为
A. | B. | C. | D. |
A
解析试题分析:因为 前
前 项和为
项和为 且
且 ,
,

所以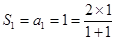 ,
, ,所以
,所以
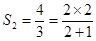 ,
,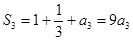 ,所以
,所以 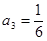
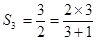 ,
,
所以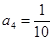 ,
, 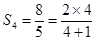 …,于是猜想:
…,于是猜想: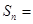
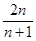 .
.
考点:数列的求和;归纳推理.
点评:本题考查了用递推公式,通过归纳推理,求数列的前n项和为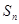 ,需要有一定的计算能力和归纳猜想能力.
,需要有一定的计算能力和归纳猜想能力.

练习册系列答案
相关题目
数列{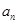 }满足
}满足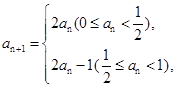 若
若 =
=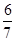 ,则
,则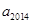 的值是( )
的值是( )
A.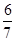 | B.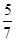 | C.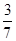 | D.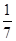 |
设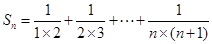
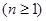 ,若
,若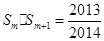 ,则
,则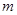 =( )
=( )
| A.2013 | B.2014 | C.4028 | D.4026 |
设S n是公差为d(d≠0)的无穷等差数列{a n}的前n项和,则下列命题错误的是
| A.若d<0,则数列{S n}有最大项 |
| B.若数列{S n}有最大项,则d<0 |
C.若数列{S n}是递增数列,则对任意的n N*,均有S n>0 N*,均有S n>0 |
D.若对任意的n N*,均有S n>0,则数列{S n}是递增数列 N*,均有S n>0,则数列{S n}是递增数列 |
将石子摆成如图的梯形形状,称数列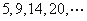 为“梯形数”.根据图形的构成,数列的第10项为( )
为“梯形数”.根据图形的构成,数列的第10项为( )


A.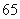 | B.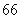 | C.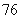 | D. |
已知
 ,已知数列
,已知数列 满足
满足 ,且
,且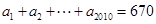 ,则
,则 ( )
( )
| A.有最大值6030 | B.有最小值6030 |
| C.有最大值6027 | D.有最小值6027 |
若数列 中,
中, ,则
,则 取得最大值时
取得最大值时 的值是( )
的值是( )
| A. 13 | B. 14 | C. 15 | D. 14或15 |
数列 的通项公式
的通项公式 ,则数列
,则数列 的前10项和为
的前10项和为
A. | B. | C. | D. |
 ,an=log2
,an=log2 ,则S2 013=________.
,则S2 013=________.