题目内容
数列{an}中,a1=1,对于所有的n≥2,n∈N*都有a1·a2·a3·…·an=n2,则a3+a5等于 ( ) .
A. | B. | C. | D. |
D
解析试题分析:∵对于所有的n≥2,n∈N*都有a1·a2·a3·…·an=n2,①,∴当n≥2时,a1·a2·a3·…·an-1=(n-1)2,②,则①÷②得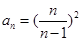 ,∴
,∴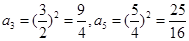 ,∴
,∴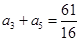 ,故选D
,故选D
考点:本题考查了数列通项的求法
点评:求数列的通项公式关键问题就是找出 与n的关系,所以只要能从给出的式子中求出
与n的关系,所以只要能从给出的式子中求出 与n的等式即可
与n的等式即可

练习册系列答案
相关题目
已知数列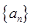 的前n项和为
的前n项和为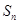 ,且
,且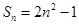 ,则
,则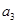 等于( )
等于( )
| A.-10 | B.6 | C.10 | D.14 |
若数列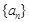 满足:存在正整数
满足:存在正整数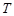 ,对于任意正整数
,对于任意正整数 都有
都有 成立,则称数列
成立,则称数列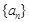 为周期数列,周期为
为周期数列,周期为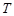 . 已知数列
. 已知数列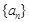 满足
满足 ,
,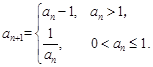
则下列结论中错误的是( )
A.若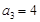 ,则 ,则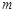 可以取3个不同的值 可以取3个不同的值 |
B.若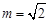 ,则数列 ,则数列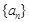 是周期为 是周期为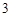 的数列 的数列 |
C. 且 且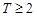 ,存在 ,存在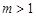 , ,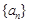 是周期为 是周期为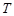 的数列 的数列 |
D.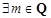 且 且 ,数列 ,数列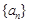 是周期数列 是周期数列 |
设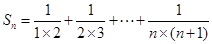
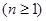 ,若
,若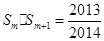 ,则
,则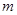 =( )
=( )
| A.2013 | B.2014 | C.4028 | D.4026 |
设S n是公差为d(d≠0)的无穷等差数列{a n}的前n项和,则下列命题错误的是
| A.若d<0,则数列{S n}有最大项 |
| B.若数列{S n}有最大项,则d<0 |
C.若数列{S n}是递增数列,则对任意的n N*,均有S n>0 N*,均有S n>0 |
D.若对任意的n N*,均有S n>0,则数列{S n}是递增数列 N*,均有S n>0,则数列{S n}是递增数列 |
已知
 ,已知数列
,已知数列 满足
满足 ,且
,且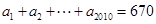 ,则
,则 ( )
( )
| A.有最大值6030 | B.有最小值6030 |
| C.有最大值6027 | D.有最小值6027 |
数列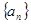 中,
中,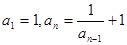 ,则
,则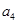 等于( )
等于( )
A.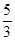 |
B.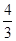 |
| C.1 |
D.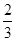 |
 的图象在点
的图象在点 处的切线的斜率为3,数列
处的切线的斜率为3,数列 的前
的前 项和为
项和为 ,则
,则 的值为( )
的值为( )



 的各项均为正整数,对于
的各项均为正整数,对于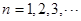 ,有
,有 ,
,  ,当
,当 且
且 为奇数时,
为奇数时, ,则
,则