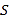题目内容
【题目】若变量![]() ,
,![]() 满足约束条件
满足约束条件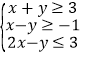 ,且
,且![]() 最小值为7,则
最小值为7,则![]() 的值为( )
的值为( )
A. 1B. 2C. -2D. -1
【答案】B
【解析】
由约束条件作出可行域,化目标函数为直线方程的斜截式,对a分类讨论可得最优解,联立方程组求得最优解的坐标,代入目标函数即可求得a值.
解:由约束条件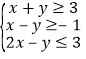 作出可行域如图,
作出可行域如图,
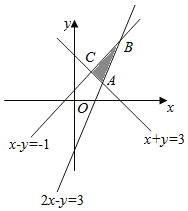
联立方程组求得A(2,1),B(4,5),C(1,2),
化目标函数z=ax+3y为y![]() .
.
当a>0时,由图可知,当直线y![]() 过A或C时,直线在y轴上的截距最小,z有最小值.
过A或C时,直线在y轴上的截距最小,z有最小值.
若过A,则2a+3=7,解得a=2;若过C,则a+6=7,解得a=1不合题意.
当a<0时,由图可知,当直线y![]() 过A或B时,直线在y轴上的截距最小,z有最小值.
过A或B时,直线在y轴上的截距最小,z有最小值.
若过A,则2a+3=7,解得a=2,不合题意;若过B,则4a+15=7,解得a=﹣2,不合题意.
∴a的值为2.
故选:B.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
【题目】为了解人们对“延迟退休年龄政策”的态度,某部门从年龄在15岁到65岁的人群中随机调查了100人,并得到如图所示的频率分布直方图,在这100人中不支持“延迟退休年龄政策”的人数与年龄的统计结果如表所示:


(1)由频率分布直方图,估计这100人年龄的平均数;
(2)根据以上统计数据填写下面的2![]() 2列联表,据此表,能否在犯错误的概率不超过5%的前提下,认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异?
2列联表,据此表,能否在犯错误的概率不超过5%的前提下,认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异?
45岁以下 | 45岁以上 | 总计 | |
不支持 | |||
支持 | |||
总计 |
参考数据:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |