题目内容
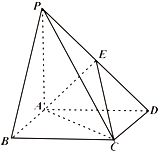
【题目】如图,在正三棱锥P﹣ABC中,D,E分别是AB,BC的中点. 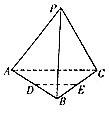
(1)求证:DE∥平面PAC;
(2)求证:AB⊥PC.
【答案】
(1)证明:∵在正三棱锥P﹣ABC中,D,E分别是AB,BC的中点.
∴DE∥AC,
∵DE平面PAC,AC平面PAC,
∴DE∥平面PAC.
(2)证明:连结PD,CD,
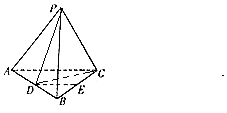
∵正三棱锥P﹣ABC中,D是AB的中点,
∴PD⊥AB,CD⊥AB,
∵PD∩CD=D,∴AB⊥平面PDC,
∵PC平面PDC,∴AB⊥PC.
【解析】(1)推导出DE∥AC,由此能证明DE∥平面PAC.(2)连结PD,CD,则PD⊥AB,CD⊥AB,从而AB⊥平面PDC,由此能证明AB⊥PC.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.

练习册系列答案
相关题目