题目内容
已知函数
(Ⅰ)求 的值域;
的值域;
(Ⅱ)设 ,函数
,函数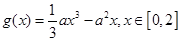 .若对任意
.若对任意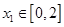 ,总存在
,总存在 ,使
,使 ,求实数
,求实数 的取值范围.
的取值范围.
【答案】
(1)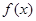 值域为
值域为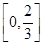 ;(2)
;(2) 的范围是
的范围是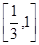
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)利用定义域和导数的符号与函数单调性的关系可知
 ,
,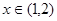
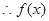 在(0,1)上单增,在(1,2)上单减
在(0,1)上单增,在(1,2)上单减
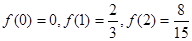 ,故
,故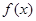 值域为
值域为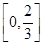
(2)因为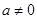 ,函数
,函数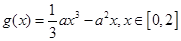 .若对任意
.若对任意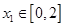 ,总存在
,总存在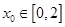 ,使
,使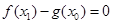 ,结合函数单调性的关系来得到分析的结论。
,结合函数单调性的关系来得到分析的结论。
解:(1) ,
,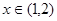 …………..
…………..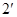
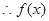 在(0,1)上单增,在(1,2)上单减
在(0,1)上单增,在(1,2)上单减
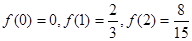 ,故
,故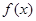 值域为
值域为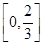 ………..
………..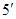
(2) ………..
………..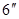
当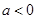 时,
时,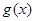 在(0,2)上单减,
在(0,2)上单减,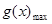 =0,不合题意;
=0,不合题意;
当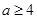 时,
时,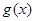 在(0,2)上单减,
在(0,2)上单减,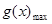 =0,不合题意; ………..
=0,不合题意; ………..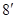
当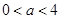 时,
时,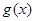 在
在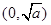 上单减,在
上单减,在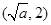 上单增,
上单增,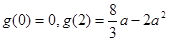
由题知: ,故
,故 的范围是
的范围是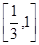 ……….
……….

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
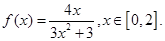
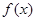 的值域;
的值域;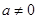 ,函数
,函数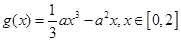 .若对任意
.若对任意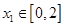 ,总存在
,总存在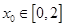 ,使
,使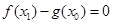 ,求实数
,求实数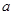 的取值范围.
的取值范围.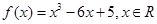
 的单调区间;
的单调区间;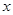 的方程
的方程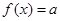 有3个不同实根,求实数
有3个不同实根,求实数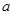 的取值范围;
的取值范围;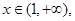
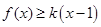 恒成立,求实数
恒成立,求实数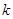 的取值范围.
的取值范围.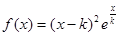 .
.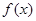 的单调区间;
的单调区间;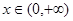 ,有
,有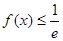 恒成立,求
恒成立,求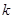 的取值范围.
的取值范围.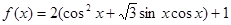 .
.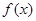 的最小正周期,并求其单调递增区间;
的最小正周期,并求其单调递增区间;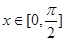 时,求
时,求 ,求
,求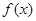 的单调区间
的单调区间